Mathematics Weblog
Polynomial Division
Sunday 19 June 2005 at 2:50 pm | In Articles | 7 CommentsA long time ago UK students used to learn how to do polynomial long division before they were 16. Nowadays, they see little of it until they reach A level, and the new national syllabus expects them to learn the remainder theorem for AS (16+). They don’t actually need to do long division as examples are usually simple enough to allow one to guess factors; for example  and
and 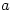 has to be found. Nevertheless, it is useful to be able to do long division and, given the time constraints, I usually use Synthetic Division.
has to be found. Nevertheless, it is useful to be able to do long division and, given the time constraints, I usually use Synthetic Division.
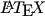 allows you not only to show the steps of either method, it will also do the mathematics for you, thanks to the polynom package. The code \polylongdiv{x^3-7x+6}{x-1} produces
allows you not only to show the steps of either method, it will also do the mathematics for you, thanks to the polynom package. The code \polylongdiv{x^3-7x+6}{x-1} produces

and \polyhornerscheme[x=1]{x^3-7x+6} gives
![\polyhornerscheme[x=1]{x^3-7x+6} \polyhornerscheme[x=1]{x^3-7x+6}](/maths/latexrender/pictures/0c5e48d1e6dc34e545214031b1df20fe.gif)
There’s lots more possibilities such as
![\polyhornerscheme[x=1,tutor=true,resultstyle=\color{blue},tutorlimit=8,stage=8]{x^3-7x+6} \polyhornerscheme[x=1,tutor=true,resultstyle=\color{blue},tutorlimit=8,stage=8]{x^3-7x+6}](/maths/latexrender/pictures/22a3dbebf1d5c92b10d574fbd7bdacb4.gif)
Brilliant! You can watch an online demo of the polynom package doing division step-by-step in a number of different ways here. Click to move the demo on, press Esc to end it.
Please note: \polyhornerscheme is not available in versions of polynom before version 0.16, so if you wish to use \polyhornerscheme do make sure you get the latest version, perhaps from here
Martin Gardner CD
Friday 10 June 2005 at 3:18 pm | In Articles | Post CommentFollow up to Martin Gardner’s Mathematical Games: The Entire Collection of His Scientific American Columns. This CD is now available at MAA Online Bookstore. As far as I know that’s the only place it’s available from which could make postage expensive for those of us outside the US – unless you know better?
Calculators
Thursday 9 June 2005 at 6:10 pm | In Articles | Post CommentThere is more emphasis these days in UK maths exams on not using calculators. This week, for example, for the first time students sat an AS exam (AS = halfway towards an A level) which didn’t allow calcuators. Many years ago when scientific calculators were first allowed questions were set that involved such large numbers that you couldn’t use a calculator directly but had to use logs.
In the US CNN.com reports that a student discovered that by pressing certain keys, they could get round the restrictions placed on them for their tests. I remember finding some years ago that statistical functions could be used on a calculator that didn’t appear to have that capabaility, provided you pressed a special button.
There’s no fooling budding mathematicians 😎
More Trig Ratios
Monday 23 May 2005 at 9:42 pm | In Articles | 6 CommentsStudents studying A level mathematics are expected to know exact values of a few trig ratios such as  (see Trig Ratios posting). But a visit to Mathworld reveals a whole world of fascinating values.
(see Trig Ratios posting). But a visit to Mathworld reveals a whole world of fascinating values.
Here are just a few of them (you may wish to try proving them)
![\cos\left(\dfrac{\pi}{9}\right)=2^{-\frac{4}{3}}\left(\sqrt[3]{1+i\sqrt{3}}+\sqrt[3]{1-i\sqrt{3}}\right) \cos\left(\dfrac{\pi}{9}\right)=2^{-\frac{4}{3}}\left(\sqrt[3]{1+i\sqrt{3}}+\sqrt[3]{1-i\sqrt{3}}\right)](/maths/latexrender/pictures/582104b66f6cfb8d988b27f2b7d58ea5.gif)


![\sin\left(\dfrac{\pi}{17}\right)=\frac{1}{8}\left[34-2\sqrt{17}-2\sqrt{2}\epsilon^*-2\sqrt{68+12\sqrt{17}+2\sqrt{2}(\sqrt{17}-1)\epsilon^*-16\sqrt{2}\epsilon}\:\right]^{\frac{1}{2}} \sin\left(\dfrac{\pi}{17}\right)=\frac{1}{8}\left[34-2\sqrt{17}-2\sqrt{2}\epsilon^*-2\sqrt{68+12\sqrt{17}+2\sqrt{2}(\sqrt{17}-1)\epsilon^*-16\sqrt{2}\epsilon}\:\right]^{\frac{1}{2}}](/maths/latexrender/pictures/d96c38bb044f64eab33ac3dacf4b476a.gif)
where 
 where the sequence of signs
where the sequence of signs  repeats with period 3
repeats with period 3
As I said, fascinating!
Thank goodness 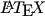 can show these values easily!
can show these values easily!
Simple?? Problem
Sunday 22 May 2005 at 7:13 pm | In Articles | 4 CommentsCan you prove that:
- if you have
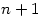 integers less than or equal to
integers less than or equal to 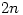 then there are always two of them which are relatively prime?
then there are always two of them which are relatively prime?This problem comes from the biography of Paul Erdös, The Man Who Loved Only Numbers. Erdös posed this problem to Louis Pósa, who was 12 at the time and a child prodigy, and who solved it in about 10 minutes.
This is one of those problems where you can spend hours getting nowhere, and yet the proof is actually very simple 😕
Mathforge
Thursday 12 May 2005 at 9:24 pm | In Articles | Post CommentMathforge is one of the best sites for finding the latest news about mathematics. It reports from what seems like everywhere to tell you what is going on in the world of mathematics. If you are interested in maths then you really should be reading it.
The site uses MathML to show the mathematics so it is good idea to install MathPlayer for Internet Explorer or add maths fonts to Firefox.
PS
Would you believe it? I have just seen that Richard Rusczyk’s the Search for Intelligence Continues. . . blog yesterday recommended Mathforge. I have been meaning to write this post for a week (honest :)) but he got there first.
I Hate Maths
Sunday 1 May 2005 at 1:08 pm | In Articles | Post CommentGooseania has started a discussion at I’m with stupid about why people hate maths (& science) but don’t have the same feelings about the Arts. Can I urge people to contribute to this fascinating topic by posting comments there?
4D Rubik’s Cube
Thursday 28 April 2005 at 11:05 pm | In Articles | Post CommentWho remembers Rubik’s cube? Rubik Unbound has an online version. Found that easy to solve? Then try the much harder 4-dimensional version at Magic Cube 4D Applet ❗
Magic Cube 4D says the normal version has 43 252 0032 274 489 856 000 unique positions whereas the 4D version has 1 756 772 880 709 135 843 168 526 079 081 025 059 614 484 630 149 557 651 477 156 021 733 236 798 970 168 550 600 274 887 650 082 354 207 129 600 000 000 000 000 unique positions, more than the number of atoms in the universe.
Similar Groups
Friday 22 April 2005 at 2:57 pm | In Articles | Post CommentStudents learning (finite) group theory often have to prove that 2 groups are isomorphic. They may construct a function from G to H, guided by their Cayley tables, then assume that the function is a homomorphism. Maybe they will check a few cases but don’t think it necessary to prove all  equations hold.
equations hold.
They are told that isomorphic groups have the same properties and, in particular, have the same number of elements of the same order. Unfortunately, they assume the converse is true which it isn’t. But the examples they see tend to confirm the converse; they don’t often see counter-examples.
To make things easier let’s say two finite groups G and H are similar if they have the same number of elements of the same order. I suspect this is entirely non-standard terminology 8-).
The counter-example of smallest order, 16, is where  and
and  which are not isomorphic (G is abelian but H isn’t) but both groups have 1 element of order 1, 3 of order 2, 4 of order 4 and 8 of order 8.
which are not isomorphic (G is abelian but H isn’t) but both groups have 1 element of order 1, 3 of order 2, 4 of order 4 and 8 of order 8.
Other examples of non-isomorphic similar groups are:
- p is an odd prime:
 which have
which have  elements of order
elements of order  and
and  elements of order
elements of order 
- p,q odd primes with
 . Let x be an element of order p and y, z have order q. Let
. Let x be an element of order p and y, z have order q. Let  and
and  . Â G, H are the semi-direct products of Q by P with
. Â G, H are the semi-direct products of Q by P with - q an odd prime such that
 . Let x have order 4 and y, z order q. Let
. Let x have order 4 and y, z order q. Let  and
and  . Â G, H are the semi-direct products of Q by P with
. Â G, H are the semi-direct products of Q by P with
G: Â  where
where 
H: Â  where
where  Then G, H are non-isomorphic groups of order
Then G, H are non-isomorphic groups of order  with
with  elements of order
elements of order  and
and  elements of order
elements of order  . The smallest such order is
. The smallest such order is 
G: Â 
H: Â  Then G, H are non-isomorphic groups of order
Then G, H are non-isomorphic groups of order  with
with  elements of order 2,
elements of order 2,  elements of order 4 and
elements of order 4 and  elements of order
elements of order  . The smallest such order is
. The smallest such order is  .
.
Norwegian mathematics
Saturday 16 April 2005 at 10:58 pm | In Articles | 7 CommentsI have been teaching Norwegian students for some years; every year it’s a new group but every year they are a pleasure to teach. Since we follow their syllabus the textbook is in Norwegian, which is fine for most mathematics but probability questions can be challenging; just a subtle change in wording can change the resulting probability.
Mathematics is a fairly universal language but there are occasional differences in Norway. In classes for British students I often use . or × for multiplication as in  or
or  , but Norwegians use · as in
, but Norwegians use · as in  and using the ‘wrong’ notation always produces complaints. Vectors are written as
and using the ‘wrong’ notation always produces complaints. Vectors are written as  rather than
rather than  , and the typed bold letter
, and the typed bold letter  is not used.
is not used.
Other interesting differences in symbols in the textbook are:
 for the unit vectors
for the unit vectors 
 for the interval from
for the interval from  to 0
to 0 In differentiation, function notation is used but I have never before seen it used as in
 or
or 
The solution of
 is written
is written 
Of course, I am assuming it’s not just the book I’m using, but as the students are comfortable with the notation I expect it’s common in Norway.
The exams are interesting. They are much longer than in the UK lasting 5 hours, so they can only have 1 exam per day. But what is really fascinating, is that to maintain national standards, externally set exams are only sat by selected students, chosen in a lottery. The students only get short notice of whether or not they have been selected and the external exam mark supersedes any internal exam marks. Different selections are made for each subject.
The standard of mathematics they have to learn is roughly equivalent to A level, but the standard of behaviour, willingness to learn and participation is far superior! They study more subjects than is common in the UK and not only do they all know who Niels Henrik Abel was, but even know his most famous result (insolubility of a quintic). Impressive. How many British students can do the same for any British mathematician? They get taught multiplication tables up to 20, which is twice as far as here in the UK and further than the 12 in my day.
Question: Can you name any other famous Norwegian mathematicians? One of them is well known for theorems in group theory. Answers below
Continue reading Norwegian mathematics…
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^