Trig Ratios

Sunday 4 April 2004 at 10:55 am | In Articles | 1 Comment

A level syllabuses these days expect you to remember the exact values of sin cos and tan of certain angles. 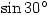\sin 30^\circ is easy enough as the calculator will give you the exact answer, but unless you know roughly what 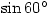\sin 60^\circ should be then the calculator will be no help.

But, help is at hand 😀 Memorising formulae is easier when there’s a pattern and the following table gives such a pattern.

\begin{array}{|c|c|c|c|c|c|} \hline \theta & 0^\circ & 30^\circ & 45^{\circ} & 60^\circ & 90^\circ \\ \hline \begin{array}{c} \\ \sin \theta \\ \\ \end{array} & \dfrac{\sqrt{0}}{2} & \dfrac{\sqrt{1}}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{3}}{2} & \dfrac{\sqrt{4}}{2} \\ \hline \begin{array}{c} \\ \cos \theta \\ \\ \end{array} & \dfrac{\sqrt{4}}{2} & \dfrac{\sqrt{3}}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{1}}{2} & \dfrac{\sqrt{0}}{2} \\ \hline \end{array}

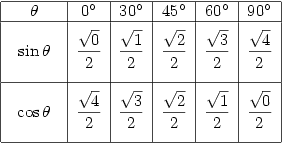
Isn’t that amazing! I only came across this a few years ago but apparently it’s been around at least since the 1950’s.

What about tan? Since 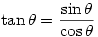\tan \theta = \dfrac{\sin \theta}{\cos \theta} you just divide a value from the second row by the one below it (but please not for 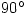90^\circ; see Tuesday 16 March).

1 Comment »

RSS feed for comments on this post. TrackBack URI

  1. Thank you! I had an instructor demo this once and I wrote it down but promptly lost it. I’ve been looking for it again for months.

    Comment by Jakob — Tuesday 24 May 2005 8:46 am #

Leave a comment

XHTML: <a href="" title=""> <abbr title=""> <acronym title=""> <b> <blockquote cite=""> <cite> <code> <del datetime=""> <em> <i> <q cite=""> <s> <strike> <strong>

Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds. Valid XHTML and CSS. ^Top^