Mathematics Weblog
Cauchy-Riemann
Friday 28 October 2005 at 2:49 pm | In Articles | 1 CommentThe Cauchy-Riemann equations are one of the first results one comes across in Complex Analysis. A poster on S.O.S. Mathematics Cyberboard has pointed that that proofs like that at Cauchy-Riemann equations tend to take it for granted that if  is analytic then the partial derivatives of
is analytic then the partial derivatives of  and
and 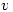 exist. Thus the proof at Cauchy-Riemann equations says
exist. Thus the proof at Cauchy-Riemann equations says
![\displaystyle f^{\prime}(z)=\lim_{h\rightarrow 0}{\left[\frac{u(x+h,y)-u(x,y)}{h}+i\frac{v(x+h,y)-v(x,y)}{h}\right]} \displaystyle f^{\prime}(z)=\lim_{h\rightarrow 0}{\left[\frac{u(x+h,y)-u(x,y)}{h}+i\frac{v(x+h,y)-v(x,y)}{h}\right]}](/maths/latexrender/pictures/da62bfe56ce08d6df3272c24f9aded5b.gif) and then deduces that
and then deduces that 
Looking at various textbooks this omission seems to the norm. Even Ahlfors Complex Analysis says: We remark that the existence of the … partial derivatives … is implied by the existence of 
One excellent book A First Course in Complex Functions by G.J.O. Jameson does give a proper proof of this result. It defines differentiability for  (where
(where 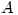 is a subset of
is a subset of  ) at a point
) at a point  in the interior of
in the interior of 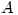 if there exists real numbers
if there exists real numbers  such that, given
such that, given  , there exists
, there exists  such that, for all real
such that, for all real  with
with  ,
, 
Putting  shows that
shows that  ; similarly
; similarly 
If  then, given
then, given  , there exists
, there exists  such that for all real
such that for all real  with
with 

and taking real parts
 from which it follows that
from which it follows that  and
and  exist. Taking imaginary parts gives the other 2 partial derivatives.
exist. Taking imaginary parts gives the other 2 partial derivatives.
1 Comment »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
I think that both the poster at SOS and you missed the point here. If exists than it follows easily that the partials exist by the fact that if one restricts oneselves to real h, than the existence of
exists than it follows easily that the partials exist by the fact that if one restricts oneselves to real h, than the existence of ![\displaystyle f^{\prime}(z)=\lim_{h\rightarrow 0}{\left[\frac{u(x+h,y)-u(x,y)}{h}+i\frac{v(x+h,y)-v(x,y)}{h}\right]}
\displaystyle f^{\prime}(z)=\lim_{h\rightarrow 0}{\left[\frac{u(x+h,y)-u(x,y)}{h}+i\frac{v(x+h,y)-v(x,y)}{h}\right]}](/maths/latexrender/pictures/701c9d66342b5bccd53fdcb33431c9d5.gif) implies that the real part of the righthand side has as limit the real part of
implies that the real part of the righthand side has as limit the real part of  (and thus the partial of u wrt x exists). This follows through the inequality
(and thus the partial of u wrt x exists). This follows through the inequality  . Similarly for the imaginary part.
. Similarly for the imaginary part.
Comment by Anton R. Schep — Saturday 12 November 2005 2:22 am #