Mathematics Weblog
Generalisation of derivative
Sunday 6 June 2004 at 2:25 pm | In Articles | Post CommentInspired by a posting on S.O.S. Mathematics CyberBoard
Most students will be familiar with the definition of the derivative of a real-valued function of a real variable defined on some interval (a,b):
- If
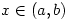 then f is differentiable at
then f is differentiable at  if
if 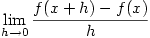 exists and the limit is denoted
exists and the limit is denoted 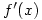
It is also clear that for this to make sense 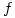 must be defined at
must be defined at  (and of course it is a well-known consequence of the definition that
(and of course it is a well-known consequence of the definition that 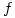 is also continuous at
is also continuous at  ). But what if
). But what if 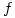 is defined on
is defined on  but not at
but not at  , can we do anything then? Yes, we can define a pseudo-derivative
, can we do anything then? Yes, we can define a pseudo-derivative  of
of 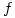 provided
provided 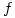 is defined on a neighbourhood of
is defined on a neighbourhood of  :
:
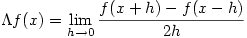
This pseudo-derivative has similar properties to the derivative and indeed it has the same values where 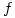 is differentiable but there are significant differences as the following exercises show:
is differentiable but there are significant differences as the following exercises show:
- If
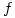 is differentiable at
is differentiable at  show that
show that 
- If
 show that
show that  exists although
exists although  does not
does not - If
 show that
show that 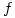 has a local maximum at 0 but
has a local maximum at 0 but 
- Suppose
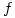 is differentiable on
is differentiable on  , except at a point
, except at a point  in
in  , with
, with  for
for  .
.
If exists show that
exists show that 
No Comments yet »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^