Mathematics Weblog
LaTeX
Sunday 30 May 2004 at 1:18 pm | In Articles | Post Comment is a very powerful language and allows one to type very nice mathematics in a way that would be difficult to do any other way. It is what provides the mathematics on this site. How else could one show
is a very powerful language and allows one to type very nice mathematics in a way that would be difficult to do any other way. It is what provides the mathematics on this site. How else could one show
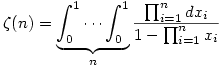
But  will do more than that and also provide graphics. See the diagram in Monday 10 May or how about these:
will do more than that and also provide graphics. See the diagram in Monday 10 May or how about these:
|
|
go on – spot the deliberate error 😕 |
or
See here for a good tutorial on  graphics
graphics
Two Interesting Functions
Sunday 23 May 2004 at 10:33 am | In Articles | 2 CommentsAt A level students only see reasonably nice functions, though occasionally they come across
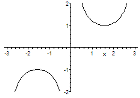
where the maximum is smaller than the minimum (which, incidentally, is why one should use the terms local maximum and local minimum instead).
But what they won’t have come across are functions like these:
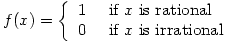

When trying to draw the graphs remember that
- between every pair of irrational numbers there is a rational number
- between every pair of rational numbers there is a irrational number
You can very roughly draw f using dots and there’s a nice picture of g at mathworld
Now think about integrating f and g – do they have areas under between them and the x-axis? The answer to ths question is important in the theory of integration.
These functions have other interesting properties and illustrate the relationship between rational and irrational numbers.
Nice Problem
Sunday 16 May 2004 at 7:28 pm | In Articles | Post CommentThere’s a very nice problem on The University of Warwick Mathematical Society’s site.
I won’t say exactly where because it has the solution there as well 😕
- If
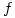 is continuously differentiable on the open interval
is continuously differentiable on the open interval 



then prove that 
Stuck!. Then click on read more for a hint
Continue reading Nice Problem…
Going dotty
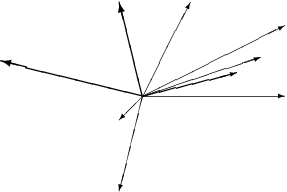
Monday 10 May 2004 at 6:59 pm | In Articles | Post CommentA well-known problem is to be given 9 dots

You have to connect the dots by using 4 lines, without taking your pen off the paper and only going through each dot once. At first sight this looks impossible until you are shown you can go outside the square formed by the dots as in
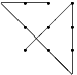
But what about 16 dots arranged in a square, or 12 dots arranged in 3 rows of 4? How many lines are needed for a 10 x 10 grid? What if arcs of circles are used instead of lines?
These and other fascinating questions about dots can be found at the web page simply called dots
Problem
Monday 26 April 2004 at 4:53 pm | In Articles | 4 CommentsFirstly, show that:
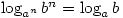
Secondly, are there any other operations you can do to 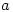 and
and 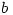 and the
and the  retains the same value? In other words:
retains the same value? In other words:
- Find all functions
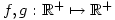 such that
such that 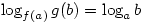 for all
for all 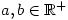
Cancelling
Tuesday 20 April 2004 at 4:27 pm | In Articles | 1 CommentStudents love to cancel wherever they can, so much so that the book Comic Sections (now out of print) had the following joke:
- The student law of universal cancellation: If the same symbol x occurs in any two different places on the one page it may be cancelled
So you get horrors like  😮
😮
And yet strange things can happen. It is true that  .
.
What is remarkable is that you can have as many sixes as you like and cancel them as many times as you like so, for example,  . Can you prove this is true? Can you find 3 other similar fractions?
. Can you prove this is true? Can you find 3 other similar fractions?
The LambertW Function
Friday 9 April 2004 at 2:35 pm | In Articles | 1 CommentMany equations cannot be solved exactly without using special functions. For example, to solve 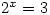 requires the use of the
requires the use of the 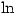 function (or similar). This function is sometimes defined in terms of an integral from which their properties can be deduced. Thus
function (or similar). This function is sometimes defined in terms of an integral from which their properties can be deduced. Thus 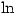 is defined by
is defined by 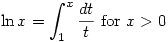 and it is then clear that, for example,
and it is then clear that, for example, 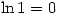
There are many equations that can only be solved in terms of newly-defined functions. One such function that isn’t all that well known is the LambertW function where 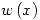 is defined as a solution (for
is defined as a solution (for 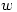 ) of
) of 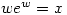 . This allows you to solve equations like
. This allows you to solve equations like 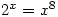 which was asked about on the S.O.S. Mathematics CyberBoard
which was asked about on the S.O.S. Mathematics CyberBoard
To solve 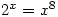 let
let 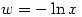 so that
so that 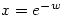 . Then
. Then
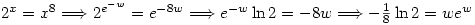
Thus 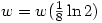 and so
and so 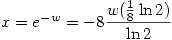 which is our answer.
which is our answer.
Using tables or software this gives 1.100.
But hang on, is that the only solution? No, because 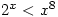 for small values of
for small values of  and
and 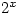 grows much faster than
grows much faster than 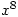 so
so 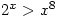 for large values of
for large values of  . Since both
. Since both 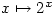 and
and 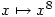 are continuous on
are continuous on 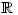 there is another value of
there is another value of  for which
for which 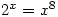 . A quick fiddle with a calculator gives
. A quick fiddle with a calculator gives 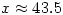 .
.
Research into the LambertW function to find out how this other solution can be given in terms of this function.
Joke
Sunday 4 April 2004 at 2:25 pm | In Articles | Post CommentJoi Ito’s Page contains a wonderful joke which I really have to repeat here.
- After explaining to a student through various lessons and examples that
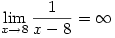
I tried to check if she really understood that, so I gave her a different example. This was the result:
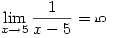
😀
Trig Ratios
Sunday 4 April 2004 at 10:55 am | In Articles | 1 CommentA level syllabuses these days expect you to remember the exact values of sin cos and tan of certain angles.  is easy enough as the calculator will give you the exact answer, but unless you know roughly what
is easy enough as the calculator will give you the exact answer, but unless you know roughly what  should be then the calculator will be no help.
should be then the calculator will be no help.
But, help is at hand 😀 Memorising formulae is easier when there’s a pattern and the following table gives such a pattern.

Isn’t that amazing! I only came across this a few years ago but apparently it’s been around at least since the 1950’s.
What about tan? Since  you just divide a value from the second row by the one below it (but please not for
you just divide a value from the second row by the one below it (but please not for  ; see Tuesday 16 March).
; see Tuesday 16 March).
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^

 ?
?