Mathematics Weblog
Amazing Formula
Monday 11 October 2004 at 9:47 pm | In Articles | 3 CommentsThere are many interesting formulae in mathematics;
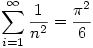
must be one of the most amazing of all.
The first reaction is where did that  come from? You can find 14 different proofs of this in a paper on Robin Chapman’s Home Page [look for Evaluating zeta(2)]
come from? You can find 14 different proofs of this in a paper on Robin Chapman’s Home Page [look for Evaluating zeta(2)]
Given this result can you prove another amazing result?
If you pick two positive integers at random, the probability of them having no common divisor is 
 gets everywhere! See Wikipedia for more such as
gets everywhere! See Wikipedia for more such as
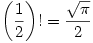 or
or 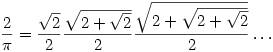 or
or 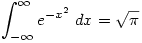
Primes
Sunday 10 October 2004 at 6:42 pm | In Articles | Post CommentEuclid’s proof that there are an infinite number of primes is a classic and as such appears as the first proof in Proofs from The Book.
Equally well-known is the formula (known as The Prime Number Theorem) which tells you that the number of primes  less than
less than  is given by
is given by  which means that the larger the value of
which means that the larger the value of  the closer (in a well-defined mathematical sense)
the closer (in a well-defined mathematical sense)  is to
is to  . This is quite hard to prove.
. This is quite hard to prove.
An easier, but non-trivial result, is Bertrand’s postulate which says that there is always a prime between 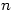 and
and 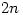 .
.
The fact that there are arbitrarily large gaps between successive primes is not difficult to prove. Suppose we want to find a gap between successive primes which is at least of size  . Then we look at the numbers
. Then we look at the numbers

Then each of these numbers is not prime. Why? Look at  where
where  . Then
. Then 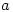 divides both
divides both  and
and 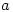 and so divides
and so divides  . Clearly
. Clearly  so
so  shows
shows  is not prime.
is not prime.
So we have a series of  numbers all of which are not prime; thus the gap between a prime less than
numbers all of which are not prime; thus the gap between a prime less than  and a prime more than
and a prime more than  is at least
is at least  .
.
Error
Saturday 2 October 2004 at 10:04 pm | In Articles | 2 CommentsSix months ago in an article on the LambertW function I wrote:
- Thus
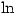 is defined by
is defined by 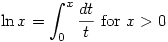 and it is then clear that, for example,
and it is then clear that, for example, 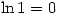
There’s a serious error in there which also completely invalidates it is then clear that …. Going back to the article the mistake leapt out at me – is it obvious to you? It’s strange how you read what you want to read rather than what is actually there 😕
Two maths problems solved??
Tuesday 7 September 2004 at 5:21 pm | In Articles | 1 CommentThe Guardian reports today, in an article with an over-the-top title of Maths holy grail could bring disaster for internet, that 2 of the seven millenium problems, the Riemann Hypothesis and the Pincaré Conjecture may have been solved.
The article links a proof of the Riemann Hypothesis, to knowing more about primes, to cracking of codes based on prime numbers. This is tenuous at best. Yes, the proof may lead to further understanding of primes, but why that means that the codes become useless is beyond me. There are many results which depend on the Riemann Hypothesis (they say things like assuming the Riemann Hypothesis is true then …) so knowing the Riemann Hypothesis is true just makes these results true. If one of these results had led to cracking of codes it would be known about now.
On the other hand if someone shows that the Riemann Hypothesis is false, then that would cause a drastic rethink in many areas of mathematics.
Fascinating fact
Sunday 18 July 2004 at 11:35 am | In Articles | Post Comment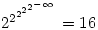
seen in announcement for EuroTeX 2005
Mathematics Blogs
Thursday 15 July 2004 at 5:56 pm | In Articles | 2 CommentsIt’s a shame there aren’t many maths blogs around, but Isabel’s math blog is an exception and is worth exploring.
I have put a newsfeed to this blog at Maths & Science Newsfeeds along with other resources.
Do you know any other good maths blogs/newsfeeds?
Powers
Friday 25 June 2004 at 3:37 pm | In Articles | 3 CommentsI was asked recently why  . Remember that if n is a positive whole number then
. Remember that if n is a positive whole number then  . Clearly you can’t multiply 2 by itself 0 times 😕
. Clearly you can’t multiply 2 by itself 0 times 😕
The key, when extending properties of the number system, is to use definitions that work for every number. So, for example
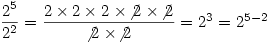
which gives you the rule that
- to divide powers you subtract the indices (the small superscripted numbers)
This leads to
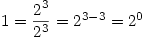
Similarly,  for any positive real number.
for any positive real number.
What about zero powers of non-negative powers?  is a controversial case I have mentioned on 29 February (Q2.) and see Dr Math FAQ for more on this.
is a controversial case I have mentioned on 29 February (Q2.) and see Dr Math FAQ for more on this.
And if the number is negative? Great care is needed in this case. For example, using only real numbers,  but
but  is not a real number. The problem arises because the general definition of a power is given by
is not a real number. The problem arises because the general definition of a power is given by  and
and  is undefined if a is negative or 0. Using complex numbers (which helps with
is undefined if a is negative or 0. Using complex numbers (which helps with  ) just makes things more complex 😕 – see Log of Complex Number
) just makes things more complex 😕 – see Log of Complex Number
Misunderstanding
Wednesday 16 June 2004 at 4:23 pm | In Articles | 1 CommentWhen teaching maths that you are familiar with, it is not easy to see why students struggle with it – indeed once the student has understood the problem, they can’t see why they had difficulty before! This means that you have to be very careful what you say in case an attentive student takes it literally.
How many times has a lecturer said “the integral of e is itself ” ? So this happens:
- Q. Find the value of
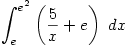
A. ![\displaystyle \int_e^{e^2}\left(\frac{5}{x}+e\right)\ dx=\left[5\ln |x| + e\right]_e^{e^2}=\dots=5 \displaystyle \int_e^{e^2}\left(\frac{5}{x}+e\right)\ dx=\left[5\ln |x| + e\right]_e^{e^2}=\dots=5](/maths/latexrender/pictures/e846d6c1a3346703ff51cd012cc2f2bb.gif)
When the error was pointed out to the student, they responded with
- Why does
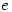 integrate to
integrate to 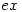 ?
? 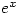 integrates to
integrates to 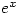 and as
and as 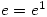 surely the integral of
surely the integral of 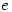 is also
is also 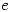 ?
?How would you respond to this?
Generalisation of derivative
Sunday 6 June 2004 at 2:25 pm | In Articles | Post CommentInspired by a posting on S.O.S. Mathematics CyberBoard
Most students will be familiar with the definition of the derivative of a real-valued function of a real variable defined on some interval (a,b):
- If
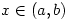 then f is differentiable at
then f is differentiable at  if
if 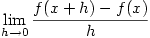 exists and the limit is denoted
exists and the limit is denoted 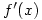
It is also clear that for this to make sense 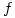 must be defined at
must be defined at  (and of course it is a well-known consequence of the definition that
(and of course it is a well-known consequence of the definition that 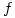 is also continuous at
is also continuous at  ). But what if
). But what if 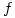 is defined on
is defined on  but not at
but not at  , can we do anything then? Yes, we can define a pseudo-derivative
, can we do anything then? Yes, we can define a pseudo-derivative  of
of 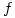 provided
provided 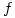 is defined on a neighbourhood of
is defined on a neighbourhood of  :
:
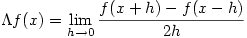
This pseudo-derivative has similar properties to the derivative and indeed it has the same values where 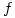 is differentiable but there are significant differences as the following exercises show:
is differentiable but there are significant differences as the following exercises show:
- If
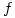 is differentiable at
is differentiable at  show that
show that 
- If
 show that
show that  exists although
exists although  does not
does not - If
 show that
show that 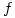 has a local maximum at 0 but
has a local maximum at 0 but 
- Suppose
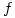 is differentiable on
is differentiable on  , except at a point
, except at a point  in
in  , with
, with  for
for  .
.
If exists show that
exists show that 
New Mersenne Prime
Monday 31 May 2004 at 2:32 pm | In Articles | Post CommentIt’s not often that one can report mathematics news but two weeks ago a new Mersenne prime was discovered. A Mersenne prime is a prime number of the form  ie one less than a power of two. It is easy to show that
ie one less than a power of two. It is easy to show that 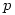 itself must also be prime. The new prime number is
itself must also be prime. The new prime number is  has 7,235,733 decimal digits and was found on a 2.4 GHz Pentium 4 computer running Windows XP.
has 7,235,733 decimal digits and was found on a 2.4 GHz Pentium 4 computer running Windows XP.
You can help search for larger primes and possibly win $100,000 for discovering the first 10-million-digit prime. See the Great Internet Mersenne Prime Search (GIMPS)
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^