Mathematics Weblog
Agnew’s Differential Equations
Sunday 5 December 2004 at 2:59 pm | In Articles | 3 CommentsWhen I studied differential equations, the set book was Ralph P Agnew’s Differential Equations. It had a brilliant index which seemed to contain every word in the book. Everything I ever wanted to look up was referenced in that index, unlike plenty of other textbooks.
It included a wonderful polemic about textbooks that claim that differential equations of order n have a general solution with n essential (aka arbitrary) constants:
- The promoted the view that to each differential equation of order n there corresponds an important family of solutions from which all other solutions … are obtainable by use of appropriate hocus-pocus involving envelopes and more complicated things. It was essential that this family of solutions should have a name (this is the start of the intimidation) which would immediately convince everybody that it existed and was important. With dubious regard for appropriateness of terminology, this family was called “the general solution” of the given equation.
He then says:
- It may be unclear whether this [differential equations of order n have n essential constants] is a theorem or a definition or merely a collection of words, but we are now in a realm where nearly everything is unclear. One thing, however, is clear. No meaning has been attached to the statement that a formula has n eseential constant. This gives the good old lecturer a chance to practice the art of proof by intimidation.
He then goes on to justify his remarks and includes as examples the differential equations 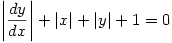 which has no solutions and
which has no solutions and 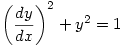 which has “vast hordes of real solutions“.
which has “vast hordes of real solutions“.
He also deals with the solution of 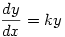 where dividing by
where dividing by 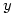 (the usual method taught at A level) won’t do since it could involve division by zero (the book indexes this as Division by zero taboo).
(the usual method taught at A level) won’t do since it could involve division by zero (the book indexes this as Division by zero taboo).
Finally, there is the wonderful snowplough problem (or snowplow as the author is American) which says:
- One day it started snowing at a heavy and steady rate. A snowplow started out at noon, going 2 miles the first hour and 1 mile the second hour. What time did it start snowing?
He says “Our first task is to recover from the shock of being asked to solve such a problem” and goes on “we assume that the plow clears snow at a constant rate of k cubic miles per hour“.
Now it’s up to you. Click on read more below for the time it started snowing.
Continue reading Agnew’s Differential Equations…
I really despair
Saturday 4 December 2004 at 8:50 pm | In Articles | 4 CommentsI came across this answer, written over a year ago, to a question about division by zero. The answer was written by a Physics instructor who seems to be rather confused.
- Division by zero is often defined as infinity. Infinity divided by zero is infinity-squared. For signs to be defined correctly, you must have a +0 and a -0. This is often accomplished through the theory of limits. The limit of x as x approaches zero from the negative side is -0. The limit of x as x approached zero from the positive side is +0. Higer (sic) level mathematics uses the concept of infinity quite often.
Let’s gloss over the first two appalling sentences. In the following sentences I suppose he is trying to refer to the fact that one can approach 0 (or any number) from different directions. If x approaches 0 from above, that is x remains positive, then you can write, for example,  . Note that the limit is written as 0 not +0 which is of course equal to 0 so there’s no point writing it! This notation allows one to show that different things can happen if x approaches 0 from above or from below and to say that
. Note that the limit is written as 0 not +0 which is of course equal to 0 so there’s no point writing it! This notation allows one to show that different things can happen if x approaches 0 from above or from below and to say that  if and only if
if and only if  (where f is a real-valued function defined on a neighbourhood of 0).
(where f is a real-valued function defined on a neighbourhood of 0).
Personally, I like using  and
and  rather than
rather than  and
and  respectively, because they illustrate the approach from above or below.
respectively, because they illustrate the approach from above or below.
Oh dear!
Tuesday 30 November 2004 at 7:38 pm | In Articles | 3 CommentsAt the risk of repeating myself, I just have to post some questions a student appears to have been asked to answer by his teacher. I say appears because the student was seeking help and may have misunderstood the questions, but I doubt it. They are horrifying.
In the following questions, say which of
- a) 0 b) 1 c)
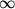 (d) indeterminate
(d) indeterminateis the correct answer:
1.  |
5.  |
9.  |
13.  |
2.  |
6.  |
10.  |
14.  |
3.  |
7.  |
11.  |
15.  |
4.  |
8.  |
12.  |
16.  |
Yes the questions do purport to be about the normal real number system. Shocking, isn’t it, that a student could be asked such drivel? 🙁
PS Just come across Not Infinity! which gives a good explanation of this type of misuse.
Wonderful quote
Wednesday 24 November 2004 at 7:27 pm | In Articles | 2 Comments- “In fact that is one of the first things we beat out of students – misapplications of equals signs, until such time as they are sufficiently well read to start abusing them again.”
matt grime at SFN
Mathematics lecturers everywhere will be nodding in agreement 😎
What does  mean?
mean?
Saturday 20 November 2004 at 5:11 pm | In Articles | Post Comment
I have written about the nonsense that comes about when you divide by 0 or attempt to use 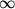 like a number. So I was delighted to come across John Conway’s comments at MathPath. John Conway is of course one of the best mathematicians today, having, amongst many other things, invented the Game of Life and discovered three sporadic finite simple groups, known as the Conway groups
like a number. So I was delighted to come across John Conway’s comments at MathPath. John Conway is of course one of the best mathematicians today, having, amongst many other things, invented the Game of Life and discovered three sporadic finite simple groups, known as the Conway groups
Nice Problem
Wednesday 17 November 2004 at 7:34 pm | In Articles | 9 CommentsHere’s a nice problem taken from ChapterZero who, in turn, got it from Rudin’s Principles of Mathematical Analysis
- Given the sequence
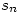 defined as
defined as 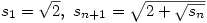 , show that
, show that 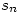 converges, and that it is bounded above by 2.
converges, and that it is bounded above by 2.More maths blogs?
Tuesday 16 November 2004 at 7:29 pm | In Articles | 4 CommentsI’ve mentioned before about a lack of mathematics blogs. Now the mathematics site Art Of Problem Solving is creating a list of blogs of members of its community.
OK, so the blogs may not be strictly mathematics blogs (mathematicians do have other interests believe it or not) but they could well be of interest to other mathematicians. Keep an eye on the blog list!
PS See also the list of Maths Blogs on the right (which is recursive 8-))
Writing Mathematics
Saturday 6 November 2004 at 8:10 pm | In Articles | 3 CommentsIsabel’s math blog is one of those rare things – a mathematics blog; let’s hope it will inspire others. Isabel is a fourth-year undergraduate mathematics student at MIT who has been marking first-year students’ homework. She makes some excellent points that are relevant at all levels including A-level.
I hope she won’t mind me quoting some of what she says at on grading homework:
- If the problem calls for some numerical answer, or for some symbolic expression as an answer, and the student produces a wrong answer, they can’t get full credit. (Very near full credit, say nine out of ten, is possible.)
- Not surprisingly, if you know what the answer to a problem is supposed to be, it’s easy to make errors that “cancel each other out”; if you know where the target is you’ll make some pretty strange logical leaps to get there. (I’ve been guilty of this too. Potential approaches to a problem that seemed incredibly stupid at noon the day before the homework is due seem quite reasonable at three in the morning.)
- The question is, how does one teach students “clarity” in mathematics? One of the things I notice is that the students don’t realize the power of the English language. They write down endless strings of equations, and make no effort to connect these with words that explain what they’re doing. Fortunately for them, as the grader I know what they’re trying to do. But at the same time, sometimes I don’t know what they’re trying to do; they manage to confuse me quite thoroughly.
There seems to be a flaw in mathematics education – that we don’t teach students how to write mathematics.
My thoughts exactly 🙂
Proof and logic
Sunday 24 October 2004 at 3:15 pm | In Articles | 3 CommentsMathematical proof is one of the topics that students find very difficult. Many of them assume what they are trying to prove, end up with a true statement and then think they have proved the result. Studying truth tables, particularly the implication operator may well help. See Logical Operations and Truth Tables
On a mathematics forum a student wanted to use its  facilities (provided by LatexRender of course 😎 ) to help a friend show how to prove
facilities (provided by LatexRender of course 😎 ) to help a friend show how to prove
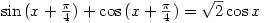
This is the original ‘proof’ they gave. Although they have now changed it I get the impression that I failed to convince them of the faulty logic; how would you explain what is wrong?
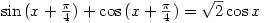
For this problem you need to know the addition formulas:

Using these formulas in the problem we can turn it into:

Then we use the fact that  and
and 
This changes it to:

Here we cancelled out the terms that equals zero and then adding together what we have we end up with:

Some textbooks misuse infinity
Monday 18 October 2004 at 3:43 pm | In Articles | Post CommentIt’s happened again! 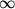 used in a textbook (unnamed to protect the guilty) as if it were a real number instead of an idea. In a discussion of the formula for the acute angle
used in a textbook (unnamed to protect the guilty) as if it were a real number instead of an idea. In a discussion of the formula for the acute angle  between two lines
between two lines
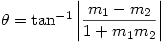
the following appears:
- Putting
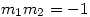 gives an angle
gives an angle 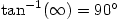 , confirming the condition for the lines to be perpendicular
, confirming the condition for the lines to be perpendicular This is of course complete nonsense. As I’ve said before  doesn’t exist and
doesn’t exist and  is only defined on
is only defined on 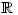 ie for
ie for 
The textbook was written by the examiners (which is one reason why we use it); this worries me even more.
I suppose this is better than one well-known textbook back in the eighties which solved the equation  by putting
by putting  then ‘showing’
then ‘showing’  or
or  . This seems to show that all linear equations are quadratics in disguise; or cubics, quartics – who knows where this nonsense leads 😕
. This seems to show that all linear equations are quadratics in disguise; or cubics, quartics – who knows where this nonsense leads 😕
See also Division by zero shock!
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^