Mathematics Weblog
Similar Groups
Friday 22 April 2005 at 2:57 pm | In Articles | Post CommentStudents learning (finite) group theory often have to prove that 2 groups are isomorphic. They may construct a function from G to H, guided by their Cayley tables, then assume that the function is a homomorphism. Maybe they will check a few cases but don’t think it necessary to prove all 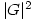 equations hold.
equations hold.
They are told that isomorphic groups have the same properties and, in particular, have the same number of elements of the same order. Unfortunately, they assume the converse is true which it isn’t. But the examples they see tend to confirm the converse; they don’t often see counter-examples.
To make things easier let’s say two finite groups G and H are similar if they have the same number of elements of the same order. I suspect this is entirely non-standard terminology 8-).
The counter-example of smallest order, 16, is where 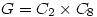 and
and 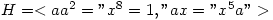 which are not isomorphic (G is abelian but H isn’t) but both groups have 1 element of order 1, 3 of order 2, 4 of order 4 and 8 of order 8.
which are not isomorphic (G is abelian but H isn’t) but both groups have 1 element of order 1, 3 of order 2, 4 of order 4 and 8 of order 8.
Other examples of non-isomorphic similar groups are:
- p is an odd prime:
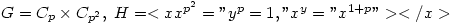 which have
which have 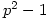 elements of order
elements of order 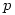 and
and 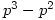 elements of order
elements of order 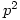
- p,q odd primes with
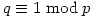 . Let x be an element of order p and y, z have order q. Let
. Let x be an element of order p and y, z have order q. Let 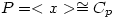 and
and 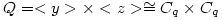 . Â G, H are the semi-direct products of Q by P with
. Â G, H are the semi-direct products of Q by P with - q an odd prime such that
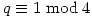 . Let x have order 4 and y, z order q. Let
. Let x have order 4 and y, z order q. Let 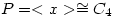 and
and 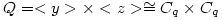 . Â G, H are the semi-direct products of Q by P with
. Â G, H are the semi-direct products of Q by P with
G: Â 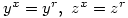 where
where 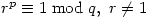
H: Â 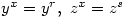 where
where 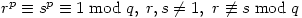 Then G, H are non-isomorphic groups of order
Then G, H are non-isomorphic groups of order 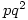 with
with 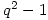 elements of order
elements of order 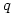 and
and 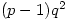 elements of order
elements of order 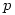 . The smallest such order is
. The smallest such order is 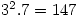
G: Â 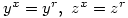
H: Â 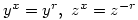 Then G, H are non-isomorphic groups of order
Then G, H are non-isomorphic groups of order 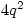 with
with 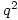 elements of order 2,
elements of order 2, 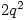 elements of order 4 and
elements of order 4 and 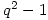 elements of order
elements of order 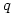 . The smallest such order is
. The smallest such order is 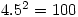 .
.
No Comments yet »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^