Mathematics Weblog

Primes

Sunday 10 October 2004 at 6:42 pm | In Articles | Post Comment

Euclid’s proof that there are an infinite number of primes is a classic and as such appears as the first proof in Proofs from The Book.
Equally well-known is the formula (known as The Prime Number Theorem) which tells you that the number of primes $\pi(x)$ less than is given by $\pi(x)\sim \dfrac{x}{\log x}$ which means that the larger the value of the closer (in a well-defined mathematical sense) $\dfrac{x}{\log x}$ is to $\pi(x)$ . This is quite hard to prove.

An easier, but non-trivial result, is Bertrand’s postulate which says that there is always a prime between 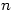and .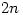

The fact that there are arbitrarily large gaps between successive primes is not difficult to prove. Suppose we want to find a gap between successive primes which is at least of size . Then we look at the numbers

$N!+2,N!+3,N!+4,\ldots,N!+(N-1),N!+N$

Then each of these numbers is not prime. Why? Look at N!+a where $2 \leq a \leq N$ . Then 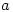divides both and 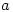and so divides N!+a . Clearly a<N!+a so $N!+a=a \times \frac{N!+a}{a}$ shows N!+a is not prime.
So we have a series of N-1 numbers all of which are not prime; thus the gap between a prime less than N!+2 and a prime more than N!+N is at least .