Another Chance to Read … Calendars

Monday 2 April 2007 at 1:56 pm | In Articles | 4 Comments

It’s not just television that thrives on repeats; I thought it worth repeating a posting about calendars from a year ago … 

It is this time of year that has attracted a lot of attention devoted to finding the dates of religious festivals. A very comprehensive calendar calculator for 25 different calendar systems can be found at Calendrica (Java applet) and details of these systems are given in a fascinating book Calendrical Calculations.

Algorithms to calculate Easter dates have been given by mathematicians through the ages, including Gauss (see for example Mind Over Mathematics: How Gauss Determined The Date of His Birth) but it does produce a few errors. In 1961 the Scottish mathematician T.H. O’Beirne published an algorithm in his Puzzles and Paradoxes column in the New Scientist subsequently reprinted in his book of the same name published by the Oxford University Press (sadly out of print but I throughly recommend looking for a second-hand copy).

O’Beirne’s algorithm (based on an 1876 article in Nature) has the merit of always giving the correct date as well as being easy to use. It is a simple exercise to write a program to do the work for you. Simple Example

O’Beirne’s algorithm
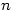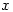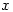The following process gives the date of Easter Sunday as the pth day of the nth month in year x. It also gives the Golden Number a+1 and the epact (23-h or 53-h whichever is between 1 and 30 inclusive). All you have to do is start with the year x and perform 10 division operations noting the quotients and remainders.

\begin{tabular}{|c|l|r|c|c|} \cline{1-5} \multicolumn{1}{|l|}{Step} & Divide & By & Quotient & Remainder \\ \cline{1-5} 1 & $x$ & 100 & $b$ & $c$ \\ \cline{1-5} 2 & $5b+c$ & 19 & - & $a$ \\ \cline{1-5} 3 & $3(b+25)$ & 4 & $\delta$ & $\epsilon$ \\ \cline{1-5} 4 & $8(b+11)$ & 25 & $\gamma$ & - \\ \cline{1-5} 5 & $19a+\delta-\gamma$ & 30 & - & $h$ \\ \cline{1-5} 6 & $a+11h$ & 319 & $\mu$ & - \\ \cline{1-5} 7 & $60(5-\epsilon)+c$ & 4 & $j$ & $k$ \\ \cline{1-5} 8 & $2j-k-h+\mu$ & 7 & - & $\lambda$ \\ \cline{1-5} 9 & $h-\mu+\lambda+110$ & 30 & $n$ & $q$ \\ \cline{1-5} 10 & $q+5-n$ & 32 & 0 & $p$ \\ \cline{1-5} \end{tabular}
(Table produced by LaTable)

4 Comments

TrackBack URI

  1. My first ever lesson in Decision 1, was to work out the day I was born using (zellers?) algorithm! Sweet- I was born on a Friday and it had all that mumbo jumbo about Fridays child being…

    Erm yeah, I just remembered that! Using algorithms can be fun, but writing them up yourself is a pain.

    Comment by beans — Monday 2 April 2007 10:36 pm #

  2. lol- I googled for the steps in Zeller’s algorithm and I was referred here!

    Comment by beans — Monday 16 July 2007 11:53 pm #

  3. […] Here is another blog, Experimental Theology by Richard Beck, which goes into a bit more detail about the astronomy AND church history behind the timing of Easter. And if that’s not enough, here’s more info for math geeks. […]

    Pingback by So, Why WAS Easter So Early This Year? « Wand’ring Through Wayne & Pike County PA — Monday 24 March 2008 3:11 am #

  4. […] entrada Another Chance to Read … Calendars do Mathematica […]

    Pingback by Algoritmo de O’Beirne, em 10 passos, para determinar o Domingo de Páscoa. « problemas | teoremas — Saturday 2 January 2010 1:09 pm #

Sorry, the comment form is closed at this time.

Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds. Valid XHTML and CSS. ^Top^