Mathematics Weblog
This site uses LatexRender for the mathematics
Going dotty
Monday 10 May 2004 at 6:59 pm | In Articles | Post CommentA well-known problem is to be given 9 dots

You have to connect the dots by using 4 lines, without taking your pen off the paper and only going through each dot once. At first sight this looks impossible until you are shown you can go outside the square formed by the dots as in
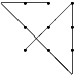
But what about 16 dots arranged in a square, or 12 dots arranged in 3 rows of 4? How many lines are needed for a 10 x 10 grid? What if arcs of circles are used instead of lines?
These and other fascinating questions about dots can be found at the web page simply called dots
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^