Mathematics Weblog
The LambertW Function
Friday 9 April 2004 at 2:35 pm | In Articles | 1 CommentMany equations cannot be solved exactly without using special functions. For example, to solve 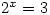 requires the use of the
requires the use of the 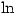 function (or similar). This function is sometimes defined in terms of an integral from which their properties can be deduced. Thus
function (or similar). This function is sometimes defined in terms of an integral from which their properties can be deduced. Thus 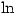 is defined by
is defined by 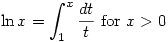 and it is then clear that, for example,
and it is then clear that, for example, 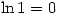
There are many equations that can only be solved in terms of newly-defined functions. One such function that isn’t all that well known is the LambertW function where 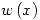 is defined as a solution (for
is defined as a solution (for 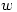 ) of
) of 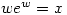 . This allows you to solve equations like
. This allows you to solve equations like 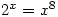 which was asked about on the S.O.S. Mathematics CyberBoard
which was asked about on the S.O.S. Mathematics CyberBoard
To solve 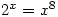 let
let 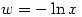 so that
so that 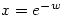 . Then
. Then
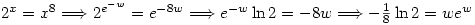
Thus 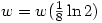 and so
and so 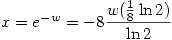 which is our answer.
which is our answer.
Using tables or software this gives 1.100.
But hang on, is that the only solution? No, because 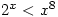 for small values of
for small values of  and
and 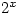 grows much faster than
grows much faster than 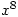 so
so 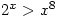 for large values of
for large values of  . Since both
. Since both 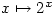 and
and 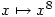 are continuous on
are continuous on 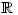 there is another value of
there is another value of  for which
for which 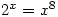 . A quick fiddle with a calculator gives
. A quick fiddle with a calculator gives 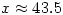 .
.
Research into the LambertW function to find out how this other solution can be given in terms of this function.
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^