Mathematics Weblog
Common Errors
Thursday 7 April 2005 at 5:32 pm | In Articles | 4 CommentsI do sometimes tend to go on and on about common errors students make, such as dividing by zero or assuming what they are trying to prove. The Most Common Errors In Undergraduate Mathematics1 is a long-standing page written by Eric Schechter. It probably contains every error that I’ve ever seen (and more) so should be required reading by all maths students.
A few errors taken at random from the page, hopefully they will encourage you to read it in more detail 🙂
Everything is additive

Everything is commutative
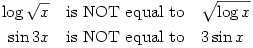
I do like this one, since it gives the right answer via multiple errors
![\displaystyle \int_0^{2\pi}\cos x \;dx=\left[\frac{\sin x}{x}\right]_0^{2\pi}=\frac{\sin 2\pi}{2\pi}-\frac{\sin 0}{0}=\sin - \sin =0 \displaystyle \int_0^{2\pi}\cos x \;dx=\left[\frac{\sin x}{x}\right]_0^{2\pi}=\frac{\sin 2\pi}{2\pi}-\frac{\sin 0}{0}=\sin - \sin =0](/maths/latexrender/pictures/cdd09e0379f65a4920df9e8dcef3be58.gif)
Oh and he has a go at teachers:
- Some teachers are hostile to questions. That is an error made by teachers. Teachers, you will be more comfortable in your job if you try to do it well, and don’t think of your students as the enemy. This means listening to your students and encouraging their questions.
Surely there aren’t many of these type of teachers about are there 😮 ?
1. Undergraduate here is an American term so the page is also highly relevant to A-Level maths students in the UK
Calculators
Friday 25 March 2005 at 2:40 pm | In Articles | 3 Commentseon has brought my attention to Tall, Dark & Mysterious’s post about the use and abuse of graphical calculators which is worth reading.
It mentions the use of calculators on mobile phones etc, but I don’t allow their use in maths classes because they give the wrong answer (try  on them or on the Windows standard calculator and you’ll see what I mean).
on them or on the Windows standard calculator and you’ll see what I mean).
The new A level syllabuses don’t distinguish between scientific and graphical calculators, but both are banned from the first Pure Maths module. It will be fascinating to see how students cope with this.
My Norwegian students all have graphical calculators (mainly Casio which I find difficult to use compared with Texas, though I like Casio’s scientific calculators) and the only way they are able to solve quadratic equations is to use the calculator, even if the quadratic factorises easily.
Other students, being students, don’t always bring calculators even when they need them. So when they have to solve  I am very tempted to give them old-fashioned four-figure tables (which you can still buy!) but instead I give them an old scientific calculator. On those, to find
I am very tempted to give them old-fashioned four-figure tables (which you can still buy!) but instead I give them an old scientific calculator. On those, to find  , you have to type
, you have to type  which so flummoxes them that they don’t forget to bring their own calculator again 😀
which so flummoxes them that they don’t forget to bring their own calculator again 😀
Online Mathematics Site
Monday 21 March 2005 at 6:17 pm | In Articles | Post CommentComputer algebra packages have developed dramatically over the years, Mathematica probably being the most well-known, though there are plenty of others – see for example the list at Wikipedia.
For those who just need to work out a problem there are also online resources. One well-known one is Integrator, which as its name suggests, will give indefinite integrals. It is important though to use the correct syntax required by Mathematica which powers the site, otherwise Integrator tells you  😕 instead of the correct
😕 instead of the correct ![\int \text{Cos}[3x]\;dx=\dfrac{1}{3}\text{Sin}[3x] \int \text{Cos}[3x]\;dx=\dfrac{1}{3}\text{Sin}[3x]](/maths/latexrender/pictures/23284b9cca66f2dcdf5b0916c26aa7b1.gif) .
.
However, I have just come across QuickMath which, although it is also powered by Mathematica, allows a more friendly input using cos(3x) rather than Cos[3x]
The site says it will do
| Algebra -Expand -Factor -Simplify -Cancel -Partial Fractions -Join Fractions |
Equations -Solve -Plot -Quadratics Inequalities |
Calculus -Differentiate -Integrate Matrices |
Numbers -Percentages -Scientific notation |
QuickMath says it has been going in various forms since 1998. How come I haven’t seen it before? It is certainly worth investigating and it will be interesting to hear how users get on with it. Are there similar sites out there?
Strange phrase
Sunday 20 March 2005 at 5:33 pm | In Articles | 2 CommentsHeard on BBC Radio 4 news last night:
- If Wales hadn’t beaten Ireland in the rugby match then it’s mathematically possible that France could have won the Grand Slam
This use of the phrase mathematically possible to mean a small probability is not uncommon, particularly in sport. And it’s not confined to the UK as Mathematically Possible shows. It would be interesting to find out how this phrase came to have this strange meaning.
LambertW
Friday 4 March 2005 at 3:09 pm | In Articles | Post CommentLast year I wrote a piece about the LambertW function. Now the American Scientist has an excellent introductory article to this function here.
The article mentions a LambertW poster you can find here.
Mathematics is Front Page News!
Wednesday 2 March 2005 at 5:59 pm | In Articles | Post CommentIt’s not often that mathematics gets onto the front page of a national newspaper but today the discovery of the latest prime has pride of place on the front page of the Guardian together with a colourful picture of some of the digits of this prime number. You can see the front page here (the story is the middle column) and read the story itself here.
Full details are at The Great Internet Mersenne Prime Search (GIMPS)
More Mathematical Humour
Friday 25 February 2005 at 3:47 pm | In Articles | 2 CommentsThe American Mathematical Society has published a paper called Foolproof: A Sampling of Mathematical Folk Humor aimed at professional mathematicians who would understand jokes like:
- Q: What do you get if you cross a mosquito with a mountain climber?
A: You can’t cross a vector with a scalar.
Q: How many topologists does it take to change a lightbulb?
A: Just one, but what will you do with the doughnut?
Q: Why did the chicken cross the Möbius strip?
A: To get to the other–er….
If you understand what Bourbaki is all about then this one is lovely:
- Q: How many Bourbakists does it take to replace a lightbulb?
A: Changing a lightbulb is a special case of a more general theorem concerning the maintenance and repair of an electrical system. To establish upper and lower bounds for the number of personnel required, we must determine whether the sufficient conditions of Lemma 2.1 (Availability of personnel) and those of Corollary (2.3.55 Motivation of personnel) apply. If and only if these conditions are met, we derive the result by an application of the theorems in Section 3.1123. The resulting upper bound is, of course, a result in an abstract measure space, in the weak-* topology.
Not heard of Nicholas Bourbaki? Then find out all about them (sic) at PlanetMath and Wikipedia
Comic Sections
Sunday 13 February 2005 at 2:53 pm | In Articles | 9 CommentsComic Sections is the funniest mathematics book I have read and I (and others) giggled all the way through it – how many maths books can you say that about? It is a collection of mathematical jokes, poems, reviews, howlers, riddles, wit etc etc which vary from the low-level
- 90° is the boiling-point of a right-angled triangle
via calculus
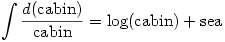
to the more advanced
- Q. What is a kittegory? A. A small category
via a journal review
- This book creates a much-needed gap in mathematics
and on to a final exam question
- Discuss the advances made in algebra since the invention of the phrase “char F
 2”
2”I have already quoted from the book a couple of times here
There’s no way I can do justice to the book so you have no choice but to buy a copy 🙂 Yes, it’s out of print but the author Desmond MacHale, will sell you one. This is what he told me:
- I have about 100 softback copies remaining which sell at a trickle because I don’t promote it and they retail at $15 US including postage if you want to spread the word about. Yes I really should rewrite it but I am busy working on Beauty in Mathematics which I hope will be influential;there are of course many new mathematical jokes since I wrote CS.One of my favourites is What is the difference between an introvert mathematician an an extrovert mathematician? Well,when an IM is talking to you he looks at his shoes;when an EM is talking to you he looks at your shoes!
My postal address is Dept of Mathematics, University College, CORK,Ireland.
Best regards, Des MacHale
PS Key in my name on Amazon.com or abebooks.com to find my other stuff on jokes,WIT,movies and lateral thinking puzzles, if you want to punish yourself further for Lent.
Blogs with Mathematics
Friday 4 February 2005 at 3:49 pm | In Articles | Post CommentIf you want to be able to create your own blog which can use  , rather like this blog, then Art of Problem Solving has recently added this facility to its forum. See here for details. You will need to register on their forum to take advantage of it.
, rather like this blog, then Art of Problem Solving has recently added this facility to its forum. See here for details. You will need to register on their forum to take advantage of it.
While you’re there, do investigate the wealth of mathematics contained in the forum – maybe you’ll be hooked 😎
Divisors
Sunday 30 January 2005 at 8:25 pm | In Articles | 2 CommentsMost people, when asked how many divisors the number 60 has (including 1 and 60), would struggle to do so without listing them all. Yet once you know that the prime factorisation of 60 is  you can immediately say that the number of divisors is
you can immediately say that the number of divisors is  . In other words, you take each index, add 1 then multiply them together.
. In other words, you take each index, add 1 then multiply them together.
This is easy to see if you list the divisors as
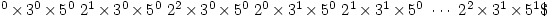
It’s then not difficult to prove the general result:
- If
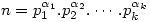 then the number of divisors of
then the number of divisors of 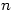 is
is 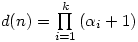
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^