Mathematics Weblog
T-shirt Slogan
Saturday 19 November 2005 at 6:57 pm | In Articles | 2 CommentsI can’t resist repeating a quote from Trevor Hawkes’ Blogging Mathematics
- We are number
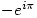
sometimes seen on mathematics students’ T-shirts.
Warwick blogs (who host Blogging Mathematics) have recently added 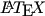 using MimeTeX to their blogs so that students and staff can blog about mathematics.
using MimeTeX to their blogs so that students and staff can blog about mathematics.
Warwick was one of the first universities to offer blogs to their staff and students and, since they have such a strong mathematics tradition (and it’s my alma mater – hi Trevor :)), it’s nice to see a maths facility.
If you want to add mimeTeX support to your blog then LatexRender (used by this blog) has an option to do so (WordPress can use the plugin at Using LaTeX in WordPress). It is better to have the full 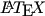 support that LatexRender also offers but that may not be possible for many bloggers, as it requires
support that LatexRender also offers but that may not be possible for many bloggers, as it requires 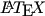 , ImageMagick and Ghostscript on the server.
, ImageMagick and Ghostscript on the server.
Another way is to install these programs on your own computer, generate the images, then upload to the server. LatexRender for Windows is a new program to help Windows users to do this.
Signature
Wednesday 9 November 2005 at 10:51 pm | In Articles | 4 CommentsPosters to forums often have signatures that are amusing and/or witty (though some are just plain daft). Few though are mathematical, but this one posted on Art Of Problem Solving’s Forum made me smile:
- The number you have dialled is imaginary. Please rotate your phone by 90 degrees and try again.
Cauchy-Riemann
Friday 28 October 2005 at 2:49 pm | In Articles | 1 CommentThe Cauchy-Riemann equations are one of the first results one comes across in Complex Analysis. A poster on S.O.S. Mathematics Cyberboard has pointed that that proofs like that at Cauchy-Riemann equations tend to take it for granted that if  is analytic then the partial derivatives of
is analytic then the partial derivatives of  and
and 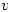 exist. Thus the proof at Cauchy-Riemann equations says
exist. Thus the proof at Cauchy-Riemann equations says
![\displaystyle f^{\prime}(z)=\lim_{h\rightarrow 0}{\left[\frac{u(x+h,y)-u(x,y)}{h}+i\frac{v(x+h,y)-v(x,y)}{h}\right]} \displaystyle f^{\prime}(z)=\lim_{h\rightarrow 0}{\left[\frac{u(x+h,y)-u(x,y)}{h}+i\frac{v(x+h,y)-v(x,y)}{h}\right]}](/maths/latexrender/pictures/da62bfe56ce08d6df3272c24f9aded5b.gif) and then deduces that
and then deduces that 
Looking at various textbooks this omission seems to the norm. Even Ahlfors Complex Analysis says: We remark that the existence of the … partial derivatives … is implied by the existence of 
One excellent book A First Course in Complex Functions by G.J.O. Jameson does give a proper proof of this result. It defines differentiability for  (where
(where 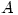 is a subset of
is a subset of  ) at a point
) at a point  in the interior of
in the interior of 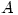 if there exists real numbers
if there exists real numbers  such that, given
such that, given  , there exists
, there exists  such that, for all real
such that, for all real  with
with  ,
, 
Putting  shows that
shows that  ; similarly
; similarly 
If  then, given
then, given  , there exists
, there exists  such that for all real
such that for all real  with
with 

and taking real parts
 from which it follows that
from which it follows that  and
and  exist. Taking imaginary parts gives the other 2 partial derivatives.
exist. Taking imaginary parts gives the other 2 partial derivatives.
Times
Saturday 22 October 2005 at 9:17 pm | In Articles | 6 CommentsAlong with other British mathematicians I am very lax about how I write the multiplication symbol. I will write
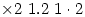
and then maintain that the context will tell the reader what is meant.
The problem comes from the fact that:
1. British students aren’t used to using the dot as a multiplication symbol – it doesn’t seem to be used in schools. They only want to use 
2. The international students have never used  (though it appears on their calculators which seem to be designed for the American market) and they are much more careful with the dot which must be on the centre of the line. They also are unhappy about the British habit of not worrying where the decimal point goes:
(though it appears on their calculators which seem to be designed for the American market) and they are much more careful with the dot which must be on the centre of the line. They also are unhappy about the British habit of not worrying where the decimal point goes:  or
or 
The students love to tell me off for using the ‘wrong’ symbol on the grounds that whatever I do is wrong 😎 It makes for very interesting discussions about the international differences in mathematics and led to a wonderful note from some of the students:
- If I insist on using . for multiplication then asking them to do Q.1 on p.77 should be read as
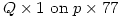 😕
😕 It’s nice to leave a class with a smile on my face.
PS For many years British students have used the word ‘times’ as in times by 3 or even worse ‘timesing’. It sounds horrible to me but I seem to have lost the battle to say ‘multiply’
Function Notation
Sunday 25 September 2005 at 6:17 pm | In Articles | 9 CommentsThe notation  is very common and is taught at A level (and sometimes earlier) in the UK. It’s well understood and used but has one well-known flaw – composition of functions.
is very common and is taught at A level (and sometimes earlier) in the UK. It’s well understood and used but has one well-known flaw – composition of functions.  or just
or just  is defined by
is defined by  . The problem here is that
. The problem here is that  means do g first then f, rather than the other way round and is therefore counter-intuitive to the beginner.
means do g first then f, rather than the other way round and is therefore counter-intuitive to the beginner.
One solution is to use a different notation for functions and use  instead of
instead of  . It’s certainly more economical to write but, more importantly, the composite function
. It’s certainly more economical to write but, more importantly, the composite function  is defined by
is defined by  , which means do f then g. This seems to be much nicer if it weren’t for one thing. As far as I know, this notation is only taught in advanced courses (3rd year degree/postgraduate) and in books like Universal Algebra by P M Cohn, which is certainly not meant to be read by a novice. By this time, the
, which means do f then g. This seems to be much nicer if it weren’t for one thing. As far as I know, this notation is only taught in advanced courses (3rd year degree/postgraduate) and in books like Universal Algebra by P M Cohn, which is certainly not meant to be read by a novice. By this time, the  is so engrained in a student’s mind it is quite difficult to change to
is so engrained in a student’s mind it is quite difficult to change to  – it certainly was for me 😕
– it certainly was for me 😕
Does anyone know if the  notation is taught in more elementary mathematics courses; if so, how was it received?
notation is taught in more elementary mathematics courses; if so, how was it received?
A Further Five Numbers
Thursday 25 August 2005 at 12:34 pm | In Articles | Post CommentBBC Radio 4 is broadcasting another series of programmes on numbers. This week’s programme features Benford’s Law which says that in naturally occurring data (so not random number tables) the number 1 appears as the first digit around 30% of the time, which is not what one would expect. It is used to detect forgeries.
You can listen to the programme at A Further Five Numbers and the rest of the series will look at 
The previous two series are also well-worth listening to; they feature  and Game Theory. They can be found at Five Numbers and Another Five Numbers
and Game Theory. They can be found at Five Numbers and Another Five Numbers
(Thanks to Gooseania)
MathWorld
Wednesday 10 August 2005 at 11:47 pm | In Articles | 4 CommentsMathWorld is a wonderful mathematics resource that is well worth browsing. It’s nice to see it has a sense of humour too – see 2001 A Space Odyssey and 42.
Does anybody know of other similar humorous entries at MathWorld or at other such resources such as PlanetMath or the maths pages of Wikipedia?
Odd one out
Wednesday 3 August 2005 at 6:38 pm | In Articles | 5 CommentsYou may well have seen those questions which ask “Which is the odd one out?”, and you often get them as part of a so-called intelligence test 😮
What the question really says is “Which one does the questioner think is the odd one out?”. So it becomes a rather more difficult test of trying to read someone else’s mind and nothing to do with your ability to solve a problem.
Here’s an example of a mathematical “odd one out” to show what I mean. Here are 4 ‘true ‘ statements:
- a. 1 + 1 = 0 true in
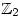 , arithmetic modulo 2
, arithmetic modulo 2b. 1 + 1 = 2 true in
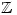 , ring of integers
, ring of integersc. 1 + 1 = 10 true in binary
d. 1 + 1 = 11 true for string concatenation in Basic
The odd one out could be
- b. because it is the only one that is true in
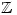
d. because it is the only one that doesn’t involve addition
a. because it is the only one where the right-hand side is less than 1 (using ordering in
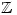 )
)c. because it is the only one where I can’t think of a reason (self-contradictory of course!)
Next time you come across one of those problems, see if you can give a reason why every one of the possibilities could be the odd one out.
Summer Reading
Monday 11 July 2005 at 5:25 pm | In Articles | 7 CommentsI finally succumbed and bought Martin Gardner’s Mathematical Games: The Entire Collection of His Scientific American Columns. Of course, as it had to be sent from America, the postage wasn’t cheap and it locked up my computer when I first tried it. Turning off CD autorun solved that problem.
Now I can spend the summer reading all those articles I’ve never read or even only half-remembered. The ability to search all the articles is a real boon. Did you know, for example, pi is mentioned 5645 times in the books?
In Fractal Music, Hypercards and More… Martin Gardner refers to the 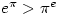 problem (which I’ve mentioned before) and says:
problem (which I’ve mentioned before) and says:
- Dozens of proofs have already been published. One of the shortest is based on the fact from elementary calculus that
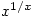 has a maximum value when
has a maximum value when  equals
equals 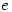 . Hence
. Hence 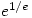 is greater than
is greater than 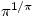 . Multiplying each exponent by
. Multiplying each exponent by 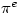 and canceling yields the inequality
and canceling yields the inequality 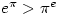 .
.The perils of publishing mathematics 😕 Can you spot the error and correct it?
Getting help
Monday 4 July 2005 at 11:08 pm | In Articles | Post CommentAt the S.O.S. Mathematics Cyberboard there’s a nice example of how students can spend all day struggling with a problem, but with a little help they can see their way to solving it in seconds. Such forums are great for getting those little nudges in the right direction that are so crucial in mathematics.
The student was trying to solve:
- For
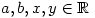 show that if
show that if 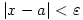 and
and 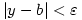 then
then 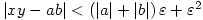
If you’ve had a go and would like the ‘nudge’ the forum provided then click here Continue reading Getting help…
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^