Mathematics Weblog

More on Maths Teaching in HE

Thanks to Gooseania for bringing to my attention a couple of interesting papers on teaching mathematics in US universities.

1. Teaching at the University Level by Steven Zucker explains how the student grading of course teaching can lead to dumbing down of courses. The teacher tends to please the student at the expense of covering the difficult parts of the mathematics course. The author believes that it would help greatly if students were to be told on arrival at university the huge difference in what is expected of them as compared to the schools they have just left.

It is unfortunate that in the UK it is so difficult to persuade non-mathematical teaching experts (so-called) that maths is hard and that I don’t expect students to understand it first-time round, which is why I spend so much time at the end of an A level course revising everything. It is true that at A level and beyond few students really understand the mathematics they have been taught until a year later (and after the exams) when they have to use it and suddenly the mist clears. I well remember looking back on a tough measure theory course that I didn’t really understand at the time, thinking ‘oh it’s obvious now’. It’s a natural part of learning mathematics and should be accepted as such.

2. Teaching Mathematics Graduate Students How to Teach by Solomon Friedberg is a paper on the usefulness of mathematical case studies for new university teachers who haven’t got the experience to judge how to pitch their courses. He gives a case study where a student argues that he should have got full marks in the following exam question (the italics are mine):

Let . Use the definition of the derivative to compute the slope of the tangent line to the graph of at the point where .

The student questions why his answer only scores 5 marks out of 20. His answer was:

, . .

The teacher fails to persuade the student of the importance of the method asked for.

Reading the question carefully and doing exactly what is asked for is a skill I have always taught A level and University students. Sometimes I even resort to “mathematics is not a democracy – you have to do as you are told” 🙂

Mathematics Teaching in HE

There’s a fascinating letter in today’s Education Guardian which I’ll reproduce here. It is a reply to a previous article by Jonathan Wolff which claims that current university teaching is poor and that lecturers need time for training.

The training is wrong
Jonathan Wolff may be speaking from his own experience with his anecdotes about poor university teaching (Comment, July 4), but in my career, teaching mathematics at four of the UK’s leading universities, I have come across very little of it.

At the London Mathematical Society we recently surveyed mathematics departments on the issue of training for new lecturers. We can confirm, with Wolff, that “barely anyone claims to having profited from it”. However, we would certainly not argue that “training is just an additional, unwelcome, burden”. Almost all our respondents agree that we need high-quality, fit-for-purpose training – but very few feel the current system provides it.
Niall MacKay
University of York

That’s precisely my experience in both HE and FE. Teacher/lecturer training in the UK is pretty awful and absolutely abysmal in mathematics, since the vast majority of trainers know very little about the subject and tend to assume that it is taught like any other subject. The word quality is over-used these days but fit-for-purpose training is exactly what is needed, but trying to explain the problem to non-mathematicians is like banging one’s head against a brick wall, so I’ve stopped trying 😕

Stretching question

A level maths questions these days vary little from year to year, so working through past papers is the best way to revise. Occasionally though, the examiners ask for something slightly different at the end of a question to separate the best students from the good ones.

This happened in this week’s Further Maths paper. It’s not hard, but the last part of the question may not have been seen by students before and so requires a little thought on their part.
The question started off with

then asked for the transformation that represents, to calculate and and then, the ‘stretcher’ for three marks, calculate .

It will be fascinating to see the examiners’ report on how students coped with this non-standard question.

The Observer’s Distribution

The front page of today’s Observer features the Poisson distribution. Why? Because some company uses it to predict the result of the World Cup. The paper seems to believe this is a newly discovered formula; in fact it was discovered by Siméon Denis Poisson in 1837. The headline says:

(…so, that’s how you find the World Cup winner)

It then spoils it all by explaining the formula with:

For those with a degree in statistics: in the equation, ‘n’ is the number of goals scored, ‘lambda’ is the expected number of goals, ‘e’ is a natural logarithm and the exclamation mark is ‘factorial’, a function of ‘n’. P is the probability distribution of goals scored. Well, we said you needed a degree.

Er, no you don’t need a degree, as the Poisson distribution is well-known to A level students; the explanation of factorial is useless but as for the definition of e, I’m speechless (for a change!).

You can find the full story here, though the headline is a mess – they should use !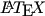

AS Maths Class 2006

The AS maths exam is on Monday, so yesterday’s class was a celebration. I must pay tribute to all of them as they have been a wonderful class, a delight to teach and I wish all of them good luck for Monday.

A Level Exam Questions

At this time of year students are going through past exam questions. It’s tough getting through the AS syllabus in time as the content is very heavy, and to make matters worse, the exam is very early (22nd May). I was somewhat relieved to see (it’s not only me having time problems), and have every sympathy for, Hannah O’Rourke who is an A level student and who writes in this week’s Education Guardian

… stop and look at your teachers. They’re usually a surprisingly good indicator of whether you should start worrying. If they look calm, cool and collected, relax. My maths A-level exams are coming up in about three weeks and we still haven’t covered three chapters in the textbook, but my teacher’s not panicking, so I’m not panicking … yet.

Revision has highlighted a problem with recent AS papers. Instead of asking you to solve a problem directly the questions take you very slowly though the method required to reach the solution, dividing it up into a number of steps. This suits British students who have been used to answering GCSE questions written in this style. But international students find it confusing, particularly if the exam insists on using a particular method. They are used to being tested for their ability to find the most appropriate method to reach a solution.

Also, one question in a recent paper tells you that then asks you to use the Remainder Theorem to find the remainder when is divided by . The question is written this way because most British students are not taught long division of polynomials. However, international students usually have a much stronger algebra background and are tempted to use long division to find the remainder. But the examiners say:

Some candidates clearly did not understand the meaning of the Remainder Theorem or the Factor Theorem and approached each of these by long division. They need to realise that when a particular method is stipulated in the question, any other approach is unacceptable.

I’m really not convinced by this – yes the Remainder Theorem is the easiest and quickest way to find the remainder, but what is wrong with using the (harder) good old long division? That technique should be encouraged.

Calendars

It is this time of year that has attracted a lot of attention devoted to finding the dates of religious festivals. A very comprehensive calendar calculator for 25 different calendar systems can be found at Calendrica (Java applet) and details of these systems are given in a fascinating book Calendrical Calculations.

Algorithms to calculate Easter dates have been given by mathematicians through the ages, including Gauss (see for example Mind Over Mathematics: How Gauss Determined The Date of His Birth) but it does produce a few errors. In 1961 the Scottish mathematician T.H. O’Beirne published an algorithm in his Puzzles and Paradoxes column in the New Scientist subsequently reprinted in his book of the same name published by the Oxford University Press (sadly out of print but I throughly recommend looking for a second-hand copy).

O’Beirne’s algorithm (based on an 1876 article in Nature) has the merit of always giving the correct date as well as being easy to use. It is a simple exercise to write a program to do the work for you. Simple Example

O’Beirne’s algorithm
The following process gives the date of Easter Sunday as the 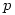^th day of the 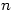^th month in year . It also gives the Golden Number and the epact ( or whichever is between 1 and 30 inclusive). All you have to do is start with the year and perform 10 division operations noting the quotients and remainders.

(Table produced by LaTable)

Exam Howlers

Have you any examination howlers? I don’t mean mistakes made by students but errors in the questions themselves, particularly those which make one wonder whether the examiner understands maths as well as they should.

My contribution is an A level question:

The function 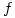is defined by and has domain

[That can’t be the tan function we all thought we knew]

The next one comes courtesy of Foostyle:

. Show where this crosses the x-axis.

[Are you sure it’s the x-axis you want?]

Your turn …

Pi Day

MathForge (a superb maths blog, worth subscribing to its newsfeed) claims that people all over the world are celebrating Pi Day since today is 3/14 which consists of the first 3 digits of the decimal expansion of . Not in the UK and other countries where the date is 14/3.

I propose an [i]e[/i] day to be celebrated on 2nd July all over the world 🙂

PS Added on 18 March
Anonymous on MathForge has just posted to say:
In fact on this side of the pond we celebrate pi day on the 22nd of July. Approximately.
Wonderful! 😀

157

Why is 157 an interesting number? The Guardian’s FE diary More than a number is not the sort of place where you would expect to find the answer. Let’s have more of this!