Mathematics Weblog

iPod Shuffle and Randomness

In an article Oh no, not Steely Dan again published in todays’ Guardian colour magazine, Steven Levy explains, in layman’s terms, why the iPod’s shuffle produces seemingly non-random results (so Steely Dan appears to be played more than other artists on his iPod) yet Apple’s engineers reassure him that the code does produce randomness.

The article has a lovely quote:

“Our brains aren’t wired to understand randomness – there’s even a huge industry that takes advantage of people’s inability to deal with random distributions. It’s called gambling.”

The way Apple dealt with this apparent non-randomness is fascinating.

The article quotes Brian Hansen’s experiments which you will find at How Much Does iTunes Like My Five-Star Songs?.

Back in the 1970s the Open University’s first level course M100 discussed the problem of defining randomness. It was usually defined in terms of probability which was itself defined in terms of randomness but it didn’t discuss Claude Shannon’s important contribution mentioned in the article. You can read more about randomness at Wikipedia.

This article (an edited extract from a forthcoming book about the iPod The Perfect Thing) should be required reading for everyone.

No it doesn’t need a maths degree!

This sort of thing rather winds me up. In an article titled “Energy switch needs a maths degree” the Guardian consumer column tries to make out that energy bills are impossible to check. It then, in a very objectionable manner, tells you how to do so. All it involves is simple arithmetic, which I would hope any GCSE student would be capable of. Why does the Guardian have to keep promoting the idea that arithmetic that uses a calculator is far too difficult for anyone without a maths degree? Perhaps they need maths teaching because they get the calculation wrong!

Here is an edited version of the article:

…you need a degree in mathematics to be able to compare the different providers accurately…
Those who have not yet lost consciousness and are eager to make their own calculations read on (this is not for the faint-hearted). Subtract the previous meter reading from the present figure. If you have an imperial meter (normally four digits) then multiply the figure by 2.83 to convert to metric. Multiply the result by 1.02264 to work out the temperature and pressure volume correction (don’t ask!). The bill will show a calorific value figure so multiply your figure by this number and if your maths is any good you should be left with 39 or 40. Divide by 3.6 to calculate how many units have been used, then multiply the units by the tariff price.

Add standing charge if applicable and 5% VAT, stir well and bake at gas mark 6. Alternatively, pour a gin and do something more interesting with your life.

What is it about our culture that so denigrates mathematics?

Here is the email I wrote to the Guardian’s consumer column. We’ll see if they take any notice.

Princeton Maths Competition

I wouldn’t normally do this, but it is always good to encourage young mathematicians so I am reproducing this email to help publicise this appeal.

Hello,

Sean Soni
Team Carolina 2006

A Differential Equation

It’s nice to see mathematics in a newspaper, but in this case it’s just there to baffle. In the printed version of today’s Guardian financial viewpoint Nils Prately wrote (the online version doesn’t include the equation):

At last, proof that PartyGaming, king of online poker, will soon find its flush busted. Here is the first line of the mathematical equation, fresh from UBS, the investment bank:

Wha’d’y’a mean you don’t get it? It’s a variation of a Lotka-Volterra differential equation for the modelling of eco-systems. Surely you’re familiar …

Lotka-Volterra consists of a pair of differential equations so how can you print just the first line 😕 it’s like printing half a word. Then again, the printed equation isn’t a differential equation – I thought perhaps was a misreading of but 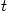seems to be the only independent variable so it’s probably . I presume there’s also another error since the equation, as printed, obviously simplifies to

The good news though is that they printed the equation using proper fonts and symbols so it did really look like mathematics 🙂

Notes & Queries

Each week the Guardian newspaper runs a Notes & Queries column where readers answer other readers’ questions. It’s been going for 15 years and often has fascinating questions and answers. I had one of my replies printed (about the VideoPlus system for numbering television programmes). It was born long before online forums became popular and spawned a number of books.

Today a question has been asked which totally astonishes me. I can’t think what the questioner thinks about mathematics.

Gravity existed before Newton discovered it. Did mathematics exist before the first mathematician evolved?

I don’t believe it is a sophisticated question about whether mathematics is invented or discovered.

If you want to answer the question, and maybe see it published, then email your (short) answer to the column at nq@guardian.co.uk

Added 27th September: In the answers given to this question (not as far as I know available online) one contributor recommends reading Conversations on Mind, Matter and Mathematics where J.-P. Changeux and Alain Connes debate questions like

Do numbers and the other objects of mathematics enjoy a timeless existence independent of human minds, or are they the products of cerebral invention? Do we discover them, as Plato supposed and many others have believed since, or do we construct them?

Mathematical Intrigue 2

Following on from Mathematical Intrigue below, a lawyer acting for Shing-Tung Yau, a mathematician mentioned in the New Yorker article, has written to the New Yorker disputing a number of points in the article and an ‘insulting’ illustration (which is not shown in the online version). You can see the Press Release with links to the letter. The letter is well worth reading. It makes many allegations of errors in the article; I found the following sentence in the letter the most interesting:

The truth is that there was no “battle” over who should receive credit for solving the Poincaré Conjecture*

This is highly unusual in mathematics – yes, people have occasionally argued about who proved what but I can’t think of a case where lawyers got involved. There’s even a webcast tomorrow Wednesday 20th September at noon, New York time.

Ars Mathematica’s article on this is worth reading. This one could run and run and is bound to be picked up by newspapers.

*The pdf’s document properties says that content copying or extraction is allowed

Web Page Puzzle

There’s a popular puzzle going round that seems to have been spread by viral marketing which gives you a web page and asks you to solve a puzzle in order to find the next page.

If you are bored then visit Hacker Puzzle and see if you can get to the final page (page 23, in case you’re wondering). Despite what it says, there’s no hacking or dodgy pages but there is some elementary mathematics.

Mathematical Intrigue

There’s a long and fascinating article in The New Yorker* about power, international politics and intrigue at the top level of mathematics connected with Grigory Perelman’s proof of the Poincaré Conjecture and his rejection of the Fields medal.

Basically Perelman, a reclusive mathematician, in 2002-3 had published an outline of a proof of the Poincaré Conjecture. In June 2006 a paper by Huai-Dong Cao and Xi-Ping Zhu says: “In this paper, we give a complete proof of the Poincaré and the geometrization conjectures“. The argument is over whether the latter paper just ‘filled in the gaps’ or is a proof in its own right.

If you thought that mathematicians are free from all the prejudices and scrambling for power that inflicts many human beings, then the New Yorker will quickly disabuse you of the fact. One of the earliest such squabbles was between Newton and Leibniz over who first invented differential calculus and it has always been so. The difference between mathematics and other spheres is that the arguments are about prestige rather than money.

*Thanks to Ars Mathematica for the link to this article

A Level Results Day

The Qualifications and Curriculum Authority, the body in charge of exams in the UK, is running a newspaper ad to show that A levels are not getting easier. They do this by reproducing exam questions. And which gets the greatest prominence by far? You guessed it – an A level maths question. This is because everyone “knows” that maths is hard and only the brightest people take it. Sigh!

       Â

The question just asks you to find the x-coordinate of the minimum point of using an iterative solution of . Of course it holds your hand through the question, as is the fashion these days as I have mentioned before.

There is some good news. The BBC report Maths resurgence follows changes says that the number of students taking A level mathematics is increasing, though sadly still at a low level. The article also says: “Another encouraging feature of the figures is that girls significantly outnumber boys among the new students.” which certainly agrees with my experience as you’ll see from the photo. The results for the pictured students were excellent – congratulations to all of them.

Menger Sponge

Maths can be fun. Students at Cornell College in Iowa have built a 3-dimensional fractal called a Menger Sponge and you’ll find a video and pictures of how they did it here.

Menger sponge

Thanks to Mathforge for the link