Mathematics Weblog
Quadratic Formula Song
Monday 24 January 2005 at 2:39 pm | In Articles | 1 CommentGot the blues about remembering  then listen to The Quadratic Formula Song at Calculus Music.
then listen to The Quadratic Formula Song at Calculus Music.
Tom Lehrer is the best known singing mathematician (zillions of pages on the net). Art Garfunkel (half of Simon & Garfunkel) will be known to older readers; he has an MA in mathematics and started a PhD but his music career came first.
A Million Random Digits With 100,000 Normal Deviates
Sunday 23 January 2005 at 11:52 am | In Articles | Post CommentMathematical humour is always welcome, particularly as it is rare. Who would have thought that a book of a million random numbers could inspire amusing reviews at Amazon.com?
Thanks to Isabel’s math blog.
Mathematical 404 Page
Sunday 16 January 2005 at 9:18 pm | In Articles | Post CommentGooseania spotted this mathematical 404 error page. Any others out there?
Four Colour Theorem Latest
Monday 10 January 2005 at 9:46 pm | In Articles | 2 CommentsListen to a short interview with Keith Devlin about the latest verification of the computer proof of the Four Colour Theorem at Solving the ‘Four-Color Problem’ of Map Making (near the bottom of the page). Then read more about it on Devlin’s Angle.
Thanks to Mathforge.net for alerting me to this.
Spherical Trigonometry
Saturday 8 January 2005 at 9:42 pm | In Articles | 8 CommentsThe idea that the angles of a triangle add up to 180° is so well engrained that it comes as a shock to some students that it isn’t true in other geometries. These geometries don’t have to be obscure or abstract since the angles of a spherical triangle drawn on the earth’s surface (assuming it is a sphere) always add up to more than 180° by an amount proportional to its area.
It’s a shame that like much else, spherical trigonometry has long since disappeared from the A level syllabus. The 2-dimensional sine rule
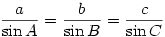
is (or ought to be 8-)) well-known but how many are aware of the 3-dimensional version
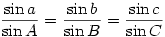
or the fact that the great circle distance (the shortest distance)  in nautical miles between points with latitude & longitude
in nautical miles between points with latitude & longitude  is given by
is given by
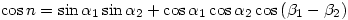
where 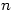 is measured in minutes? You could use sites such as Surface Distance Between Two Points of Latitude and Longitude but it’s not the same as sitting down and proving the general result.
is measured in minutes? You could use sites such as Surface Distance Between Two Points of Latitude and Longitude but it’s not the same as sitting down and proving the general result.
Without this introduction to three dimensions how is one going to start visualising geometry in four or more dimensions? Of course, reading Flatland would be an excellent start. Phoenix-Library has some excellent versions of this book in a number of online formats.
This is perhaps a suitable place to publicise my all time favourite puzzle:
- A hunter leaves his house one morning and walks one mile due south. He then walks one mile due west and shoots a bear, before walking a mile due north back to his house. What colour is the bear?
Martin Gardner’s Mathematical Games: The Entire Collection of His Scientific American Columns
Tuesday 28 December 2004 at 3:53 pm | In Articles | 10 CommentsMartin Gardner was an inspiration to many of us with his Scientific American articles. I remember devouring them avidly when I was at school many, many years ago. Some of the articles were published in various books, but now all of his columns are about to be published by The Mathematical Association of America on CD-ROM in February. American readers can pre-order it from Barnes & Noble and more details are available from Mathpuzzle.com.
Being able to read all his columns would be wonderful but I would still prefer to read it on old-fashioned paper. If it were published as a book in the UK, I would be the first to buy it.
In 1964, Scientific American devoted a complete issue to mathematics, so Martin Gardner devoted his column to word play
- … not discussed in any mathematical books, yet it has a about it a quasi-mathematical air … perhaps the combinatorial aspect is the reason why so many mathematicians are addicted to language play.
A few teasers he set from that issue:
- 1. The letters omitted from these common English words are all consonants
- _ _ _ E _ _ _ _ _
- _ A_ E _ I O U _ _ Y
2. I never did manage to find the missing letters (vowels or consonants) in
- _ _ M N O P _ _ _ _
3. He didn’t mention this word where the missing letters are again all consonants
- _ _ Y _ _ _ _
Billions of ’em
Friday 24 December 2004 at 12:10 am | In Articles | 5 CommentsI’ve long regretted the demise of the ‘British’ billion 1012, a million million, in favour of the US version which is 109, a thousand million. It means that the prefixes bi (billion), tri (trillion=million million million), quad (quadrillion) etc no longer make much sense. The change in the system is apparently due to the US adopting the French system (though France and French-speaking parts of North America changed again from 1948); international trade then did the rest. It’s all clearly explained at A Zillion Troubles (thanks to Gooseania for the link).
I sometimes ask my students to think about the size of numbers like a million and a billion (either version) by asking them to guess how long it would take to count to them at the rate of one per second without a break. Then they work it out on a calculator and 99% of their guesses are wildly out 😕
A Finite Discussion of Infinite Numbers
Wednesday 22 December 2004 at 11:03 pm | In Articles | 1 CommentKeith Devlin (British-born author of a number of interesting, well-written and highly recommended books) gives a 5-minute interview on NPR (a US radio station) about infinite numbers such as cardinal numbers like  You can find the interview at A Finite Discussion of Infinite Numbers
You can find the interview at A Finite Discussion of Infinite Numbers
Simon Singh did a couple of series of short programmes about numbers on the BBC in March 2002 and October 2003. You can listen to his discussion of Infinity; there are links there to the other broadcasts as well as to other Science programmes. Worth listening to.
Some(6,7,8,9??) years ago there was a BBC radio series on the history of mathematics which was had me rolling about as it was so (intentionally) funny. Anyone remember it or know if it is available anywhere?
Student Howlers
Saturday 18 December 2004 at 8:06 pm | In Articles | 4 CommentsA couple of howlers seen in sci.math newsgroup some years ago
1. I do like the lateral (?) thinking behind this one 😀
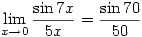
2. Problem
- Find
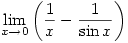
Answer
- Undefined
Proof:
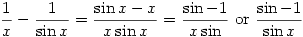
Therefore, since there are two possible answers with
 in the denominator and you can’t get rid of it and since
in the denominator and you can’t get rid of it and since 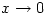 , the answer is undefined
, the answer is undefinedCancelling gives an example taken from Comic Sections by Desmond MacHale. Another one from the same book is:
3. Solve 
Solution:
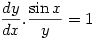 so
so 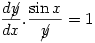 hence
hence 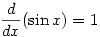 thus
thus 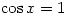 and
and 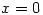
Do you have any favourite howlers?
2 unrelated problems
Sunday 12 December 2004 at 2:26 pm | In Articles | 2 Comments- Using the Gelfond-Schneider theorem show that if
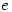 is transcendental then
is transcendental then  is transcendental
is transcendental - If
 are positive integers such that
are positive integers such that  and
and  is even, show that
is even, show that  is not a square
is not a square
Notes
- This theorem was being discussed at a seminar many years ago as was the transcendence of
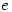 . When we were told that it was an obvious consequence that
. When we were told that it was an obvious consequence that  is transcendental we thought that the speaker was joking. When he showed how it followed, there was a moment’s silence and then applause – one of those moments when one realises that mathematics is such a wonderful subject.
is transcendental we thought that the speaker was joking. When he showed how it followed, there was a moment’s silence and then applause – one of those moments when one realises that mathematics is such a wonderful subject.
You can find an elementary proof (not using Gelfond-Schneider) of the transcendence of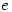 and
and  here
here
It’s interesting to note that and
and 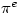 are very close. In fact
are very close. In fact  . See here
. See here - I came across this problem when looking through some old papers. I have no idea where it comes from (an old Mathematical Olympiad problem maybe??) or what the solution was.
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^