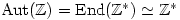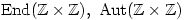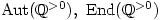Mathematics Weblog
A Levels
Monday 20 August 2007 at 11:38 am | In Articles | 12 CommentsLast Thursday the A level results were announced and there were the usual recycled comments with some people attacking and others defending the system. There appears to be three main arguments used:
- A levels are getting easier;
- Teachers are getting better at preparing students for the exams;
- Students work very hard and so it is insulting to them to say the exams are getting easier.
So let’s examine these arguments for A level maths, which is the subject I know about. Unlike some pundits I don’t wish to pontificate about subjects I am not familiar with. My main point is that the arguments above are not contradictory and it is quite possible for exams to be easier than in previous years and for students to find them hard.
- It is generally acknowledged in the mathematical community that A level maths exams are getting easier and it has been remarked on by a government advisor A-levels are easier says adviser. Yet this headline is misleading because it is only referring to maths and physics which shows just how difficult it is to have a rational argument about the standard of A levels.
It is interesting to see the effect this is having on university mathematics courses even in the last few years A-Levels: Gah.
However, A level mathematics and its equivalent has become steadily easier over at least the last hundred years as the subject has been ‘democratised’ and taught to a wider population. I am very much in favour of this but the cost has been the dumbing down of the syllabus as I have mentioned before. I can only repeat my question thatIs it possible to teach mathematics to a larger range of students without compromising on the level taught?
- This is true but nothing to be proud about. Teachers and schools are under extraordinary pressure to get good results. Hence they teach very much to the exams, test and retest, and have no time to explore interesting parts of mathematics which would help to motivate and put things into context.
How politicians can imply that this is good beats me. - Mathematics, as those of us who taught it know, is hard. This has been recognised (finally) by recent research, and it has been proposed that, as happens in Australia, more UCAS points are awarded for harder subjects like maths, though I can’t see that it will happen here.
Also mathematics is essentially linear so unless students are adequately prepared at one stage they will find it very difficult to proceed to the next stage. With dumbing down going right back to the early years of education most students will find each stage hard no matter what the level. The ignorance of this caused disaster in 2000 when A level maths was temporarily made tougher and so the gap from GCSE was unbridgeable for many students, leading to lots of failures, the abandonment of the subject by many and the restoration of an easier system.
Finally, with a greater percentage of the student population studying mathematics many of them are bound to find the subject hard.
It is good that Further Mathematics is becoming more popular and is to be encouraged, though it should be noticed that it too is a pale reflection of when it was last popular.
I don’t have easy answers to the problems of mathematical education but wish to see an informed debate on it. I just hope that Alexander Borovik is not correct when he writes
The current crisis in mathematics teaching is a dawn of a much more serious crisis of transition from the mass mathematics education of the past to a more selective and elitist education of increasingly small, in relative terms, numbers of mathematicians.
Diagonal Stripes in Group Table
Tuesday 14 August 2007 at 3:42 pm | In Articles | 5 CommentsOne of my student’s attention was drawn to the fact, that in cyclic groups of order 4 and 5, it is possible to arrange the elements so that the transverse diagonals (that is those perpendicular to the leading diagonal) of the group (Cayley) table consist of equal elements. The groups in question were 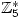 with multiplication modulo 5 and
with multiplication modulo 5 and 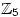 with addition modulo 5. Thus you get the following diagonal patterns highlighted by the colours:
with addition modulo 5. Thus you get the following diagonal patterns highlighted by the colours:
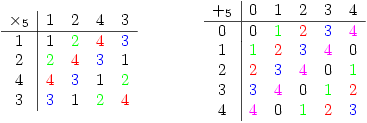
He asked 2 questions:
1. Can the elements of all (finite) cyclic groups be arranged to give these diagonal stripes?
If you take a finite cyclic group generated by the element 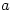 (we will use multiplication for the binary operation) then the natural ordering
(we will use multiplication for the binary operation) then the natural ordering 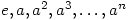 will show this pattern:
will show this pattern:
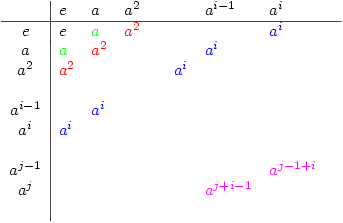
2. Are the cyclic groups the only ones that generate these patterns?
The answer is yes, but is not quite so obvious although not difficult to prove. Suppose a (finite) group G arranged as 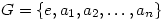 exhibits the diagonal stripes. Use induction. Let
exhibits the diagonal stripes. Use induction. Let 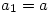 and suppose also that
and suppose also that 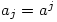 for
for 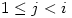 . Then we get:
. Then we get:

It follows that 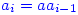 so by induction assumption,
so by induction assumption, 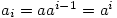 and hence
and hence 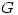 is the cyclic group generated by
is the cyclic group generated by 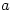 .
.
Mathematics Summer School in Sirince in Turkey
Saturday 4 August 2007 at 11:15 am | In Articles | 2 CommentsThose of us involved in mathematics education often whinge about current standards, the lack of enthusiasm in students etc so it is refreshing to read Alexander Borovik’s reports Gold Sand in a Stream and Photos from Mathematical Village about a mathematics summer school for undergraduate students in Sirince in Turkey. The summer school was run by Professor Ali Nesin, who is Chair of the Department of Mathematics of the Istanbul Bilgi University. Professor Borovik was enchanted not just by the beautiful setting but also by the ‘bright motivated students’.
The level of education was high including a crash course in reflection groups. One of the blackboards photographed includes the following mathematics:
If
is a group then the set
of automorphisms of
forms a group under composition. If
is abelian then
.
Homework:
Find
Show that ifthen
 Â
But then the story goes sour. The authorities have closed the summer school – see A Blackboard under Arrest, A Blackboard under Arrest, II  – which is such a shame. There is a petition to save the school at Save Mathematical Summer School you may wish to support, but also, can I ask other bloggers, mathematical or otherwise, to spread the news in the hope that it will help find some way round the problem?
Carnivals of Mathematics
Wednesday 6 June 2007 at 5:26 pm | In Articles | 8 CommentsThe Carnival of Mathematics is a fortnightly look at mathematical blogs. As I have commented before the growth in such blogs has been phenomenal recently which is very welcome. The carnivals are thus a gateway to the treasures that are out there, so I think it worth listing the carnivals so far (all numbers are approximate, mathematicians can count badly 🙂 ):
- Inaugural Edition hosted by Abstract Nonsense has 19 assorted links ranging from quotes exhorting people to study mathematics to algebraic topology.
- The Second Carnival Of Mathematics: The Math Geeks are Coming to Town! hosted by Good Math, Bad Math has 27 fascinating assorted links including the Halting problem, Using math for astronomy and Rubik’s Magic Cube.
- Carnival Of Mathematics #3 hosted by Michi’s Blog has 20 articles grouped into five ‘halves’: didactic, financial mathematics, humour, dimensions, and number theory, geometry, topology, algebra.
- Carnival of Mathematics Number 4 hosted by EvolutionBlog has 21 links from the Bernouilli process to finding the last two digits of 31000.
- Carnival of Mathematics, Ordinal 5 hosted by Science and Reason is dedicated to the memory of Paul J. Cohen with tributes and discussion of his work. There’s at least 30 links to other topics including tilings, Lie groups etc and surreal numbers.
- The Carnival of Mathematics Sixth Edition hosted by Modulo Errors has 19 links with many presenting problems of various difficulty.
- Carnival of Mathematics Edition #7 hosted by nOnoscience has 28 links from Euler to German bloggers and includes a new improved number system and a calculus paradox.
- 8th carnival of mathematics hosted by The Geomblog has 20 links with “time to revisit, reflect, and ponder on things we think we already know” so has an educational section and is the first carnival to have a cartoon.
- Carnival of Mathematics IX hosted by JD2718 is an alphabetical list of 36 links that appeal to the school teacher blogger.
- The next carnival is due on 15th June at MathNotations. Carnival 11 is due to be hosted by Grey Matters on 29th June and Carnival 12 on 13th July by Vedic Maths Forum. Do let them know if you have anything you wish to be included.
That’s over 200 links (not all mutually exclusive) – mathematical blogging is alive and well.
Mathematics Comedy Videos
Sunday 3 June 2007 at 11:21 am | In Articles | 9 CommentsMathematical humour is quite difficult to do. I have previously blogged about the book Comic Sections and there are other books like Carl Linderholm’s Mathematics made difficult and Ian Stewart‘s books which contain much humour; a cartoon series Ian drew is the inspiration for this

Mathematical humorous videos are even rarer. Here are a couple. The first is very well-known and has been written about all over the net for a long time. It is Finite Simple Group of Order Two by the Klein Four Group and involves very clever use of mathematical terms. The other is G103 which is described as a (surreal) day in the life of an undergraduate on the 4-year MMath degree at the University of Warwick. Anyone who has experience of a pure mathematics degree will recognise the accuracy of the amusing observations it makes. There’s more about the film at the G103 site.
There was also a previous humorous video made at Warwick University called Maths Club. Unfortunately, it’s not available on that page or anywhere else as far as I can see. Does anyone know if it’s still available?
Links to other amusing mathematics videos are very welcome.
PS The Unapologetic Mathematician links to a spoof basic mathematics tutorial produced by the BBC called Look Around You – 1 – Maths.
Dr Who’s Happy Primes
Saturday 19 May 2007 at 8:34 pm | In Articles | 1 CommentIt’s so nice to see mathematics playing an important part in popular television. In tonight’s Dr Who the spaceship crew had to find the next number in the sequence 313, 331, 367, …. Dr Who recognises this as a sequence of happy primes with the next one being 379. It’s all explained at that Wikipedia article and a longer version of the sequence can be found at the wonderful The On-Line Encyclopedia of Integer Sequences.
It’s interesting that the Dr Who reference was put in the Wikipedia article half-an-hour before the programme was aired so probably an inside job. I was delighted that in the programme Dr Who asked if mathematics was so dumbed down that recreational maths wasn’t studied any more. As Russell T. Davies, the head writer, said in tonight’s Dr Who Confidential, the programme reflects current concerns, so this problem has clearly reached a wider audience than I imagined was the case.
Eigenvalues without determinants
Friday 18 May 2007 at 3:14 pm | In Articles | 9 CommentsMost (all?) undergraduate courses use determinants to introduce eigenvalues and eigenvectors. So the eigenvalues of a matrix 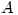 (or linear transformation
(or linear transformation 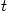 ) are the solutions of
) are the solutions of 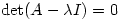 . However, Sheldon Axler published a paper in 1994 called Down with Determinants! where he maintains that determinants should not be used so early in linear algebra courses. He gives a very nice proof of the existence of eigenvalues in finite-dimensional vector spaces (over
. However, Sheldon Axler published a paper in 1994 called Down with Determinants! where he maintains that determinants should not be used so early in linear algebra courses. He gives a very nice proof of the existence of eigenvalues in finite-dimensional vector spaces (over 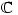 ) which I would like to reproduce here.
) which I would like to reproduce here.
Every linear transformation of a finite-dimensional complex vector space has an eigenvalue.
Here is his proof:
Let 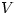 be a non-trivial finite-dimensional complex vector space and t a linear transformation
be a non-trivial finite-dimensional complex vector space and t a linear transformation 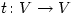 . Let
. Let 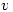 be a fixed non-zero vector in
be a fixed non-zero vector in 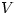 and suppose that
and suppose that 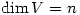 . Then the
. Then the 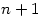 vectors
vectors 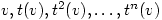 are linearly dependent. Hence there exists complex numbers
are linearly dependent. Hence there exists complex numbers 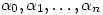 not all 0 such that
not all 0 such that
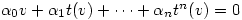 .
.
and hence
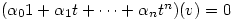 .
.
Now, since 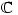 is algebraically closed, Â the polynomial
is algebraically closed, Â the polynomial 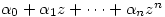 will factorise so we get
will factorise so we get
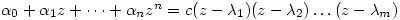 .
.
where  are complex numbers with
are complex numbers with 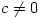 . It follows that
. It follows that
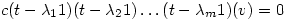
which means that, since this is composition of functions, and 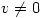 , then
, then
either
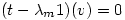 so Â
so    so that
 so that 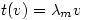 and
and 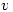 is an eigenvector
is an eigenvector
or
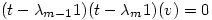 so
so 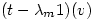 Â is an eigenvector
 is an eigenvector
or
…
or
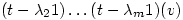 is an eigenvector,
is an eigenvector,
and hence 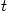 has an eigenvalue. Â Â
has an eigenvalue. Â Â 
Discussion on this approach of not using determinants can be found at NeverEndingBooks and The n-category Café.
Problems, Problems
Saturday 5 May 2007 at 2:22 pm | In Articles | 3 CommentsThe Art of Problem Solving (AopS) site encourages, teaches and promotes mathematics competitions from small local ones right up to the International Mathematical Olympiad (IMO). As it says on its front page:
Is math class too easy for you? Looking for a greater challenge?
You’ve come to the right place.
It has an excellent introduction to  site and a forum to discuss problems. The forum has an RSS feed where students pose new problems every day. So if you’re “looking for a greater challenge” subscribe to this feed. Here is a random sample of some of the problems posed recently, which range from very easy to extremely difficult. Click on the problem number to go to the discussion on it.
site and a forum to discuss problems. The forum has an RSS feed where students pose new problems every day. So if you’re “looking for a greater challenge” subscribe to this feed. Here is a random sample of some of the problems posed recently, which range from very easy to extremely difficult. Click on the problem number to go to the discussion on it.
- 1. We define addition in a different way to usual; an addition statement is true only if the letters in the addends is a rearrangement of the letters in the sum. For example,
10 + 6 = 16?
TEN + SIX = TENSIX = SIXTEN, but to be 16 it would need another E.
Find a “true” addition a + b = c + d.
2. Prove that 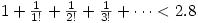 .
3. Let
.
3. Let 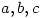 be nonzero real numbers. Find all ordered pairs
be nonzero real numbers. Find all ordered pairs 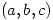 such that
such that 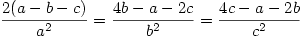 .
.
4. 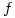 is a continuous complex-valued function satisfying:
is a continuous complex-valued function satisfying:
i) 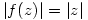
ii) 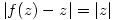
Find 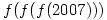
5. If 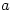 and
and 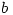 are relatively coprime, find all possible values of
are relatively coprime, find all possible values of 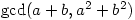 .
.
6. Let 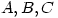 be three angles ofÂ
be three angles of 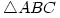 . Prove that
. Prove that  .
.
7. For each function 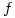 which is defined for all real numbers and satisfies
which is defined for all real numbers and satisfies 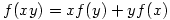 and
and 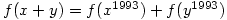 determine the value of
determine the value of 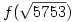 .
.
8. Let 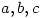 be positive reals such that
be positive reals such that 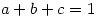 . Prove that
. Prove that 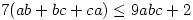 .
.
9. For 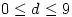 , we define the numbers
, we define the numbers 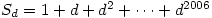 . Find the last digit of the number
. Find the last digit of the number 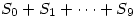 .
.
10. The product of several distinct positive integers is divisible by 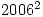 . Determine the minimum value the sum of such numbers can take.
. Determine the minimum value the sum of such numbers can take.
Equation Wizard
Sunday 29 April 2007 at 5:43 pm | In Articles | 7 CommentsI have an ambivalent attitude to mathematical software. On the one hand, an enthusiastic user of LaTeX both here and in documents and presentations, but, on the other hand, wary of too much reliance on calculators and computers. One superb maths teacher I know was criticised for not using a computer in his A level class. A Chinese student in the class remarked that they didn’t see much benefit in using one and they had only started to use a calculator when they came to this country to study A levels. They have an important point; I recoil when I ask a simple arithmetic question and the student instinctively reaches for their calculator. Worse still is when they use the calculator on their phone and don’t believe me when I tell them the calculator gets it wrong because it doesn’t obey basic mathematical rules. Similarly, I find graphics calculators are too complicated (computer programs are much easier to use to sketch graphs) and I would prefer to teach students how to sketch curves so that they get a feel for the properties of various functions.
Of course there is a place for calculators and mathematical software. Checking my tax would be a pain without a calculator and graphing software for focusing in at what happens near the origin of the graph of functions like
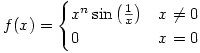
is fascinating. Similarly, if I am marking student work I use mathematical software to check their matrix operations rather than doing them by hand. Some mathematical software is very powerful and expensive but there are free sites like QuickMath which will solve many problems. However, they should really be used to save time or offer insights after the techniques have been taught and understood – practice, practice and practice is often the best way to learn.
So when I was asked by ElasticLogic to review their Equation Wizard  I made it clear that I would be offering an honest opinion of the program that they sent me.
Equation Wizard is a Windows only program that solves real rational equations and simplifies rational expressions (rational means ratios of polynomials). In fact it claims to solve algebraic equations but that is a misnomer as it doesn’t solve equations involving fractional powers or complex coefficients, though it will give some complex roots (for some reason called imaginary roots in Help). QuickMath does this for free but Equation Wizard’s strength comes from the fact that it will show the working so the user can understand the method behind the solution.
Entry of polynomials is easy using ^ for powers or using buttons or menus or the Ctrl key and the text is previewed in mathematical form as you type, so x^2 becomes 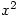 and (x^2-1)/2 becomes
and (x^2-1)/2 becomes 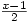 ; the previewer does its best to interpret ambiguous expressions such as 1/2x. It will add algebraic fractions showing the working, so if you input 1/(x-1)+1/(x+1) then it is simplified to
; the previewer does its best to interpret ambiguous expressions such as 1/2x. It will add algebraic fractions showing the working, so if you input 1/(x-1)+1/(x+1) then it is simplified to 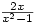 by adding using a common denominator, multiplying out and collecting the terms in the numerator to get the result, with all steps shown. It uses a similar method to solve the equation 1/(x+1)+1(x+1)=1 finding the answer to 3 decimal places (or up to 9 decimal places if required). There appears to be no limit to the degree of the polynomial equations to be solved – solving
by adding using a common denominator, multiplying out and collecting the terms in the numerator to get the result, with all steps shown. It uses a similar method to solve the equation 1/(x+1)+1(x+1)=1 finding the answer to 3 decimal places (or up to 9 decimal places if required). There appears to be no limit to the degree of the polynomial equations to be solved – solving 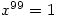 was virtually instant.
was virtually instant.
However, there are limitations. The answers given cannot give exact values so 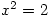 gives 1.414 and -1.414 rather than
gives 1.414 and -1.414 rather than 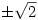 . Rational equations are solved by multiplying by the denominator but the solutions aren’t checked so
. Rational equations are solved by multiplying by the denominator but the solutions aren’t checked so 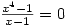 gives
gives 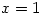 as one of four solutions. My Norwegian students were taught to always check their answers, so would know what to do. On the other hand solutions can be missed so
as one of four solutions. My Norwegian students were taught to always check their answers, so would know what to do. On the other hand solutions can be missed so 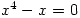 gives 0 and 0 as the two solutions, though I expect that’s just a bug. However,
gives 0 and 0 as the two solutions, though I expect that’s just a bug. However, 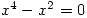 gives one correct answer and two wrong ones, which is rather worrying. There are language problems with
gives one correct answer and two wrong ones, which is rather worrying. There are language problems with 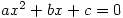 being described as a quadric equation. Quadric surfaces are interesting and there are nice pictures here.
being described as a quadric equation. Quadric surfaces are interesting and there are nice pictures here.
You can print out the calculations or save them in rtf or HTML format (with the equations saved as images) but it would be nice to be able to copy the selected output to the clipboard. Having solved an equation it’s not possible to change it – you have to enter a new one, though you can copy and paste the old one or use the history button, bizarrely labelled  .
.
Your opinions on Equation Wizard are welcome and I hope ElasticLogic will improve this early version as a result of feedback from you. Can you find other equations with missing or incorrect solutions? The software costs $29 (or £15.55 in real money 🙂 ) and you can download a free trial version here.
Mathematics in the News
Tuesday 24 April 2007 at 7:11 pm | In Articles | 11 CommentsToday the BBC reports two stories about mathematics
-
Chancellor reveals maths weakness. Gordon Brown, almost certain to be the next Prime Minister, said he wasn’t very good at maths. But he also added
“I did maths at school and for one year at university but I don’t think I was ever very good at it – and some people would say it shows,” Mr Brown laughed.
I wish he hadn’t laughed (was that due to guilt?) but in his defence he has probably studied mathematics to a higher level than most politicians. It should also be noted that he was educated in Scotland where the first year of university is the equivalent to the last year of school in England and Wales (and so is more like the US system). So he is likely to have studied mathematics to A level standard.
Pupils are being discouraged from taking A-level maths as schools in England chase higher places in the league tables, scientists have claimed.
The Royal Society of Chemistry said that as maths was a difficult subject, schools feared examination failures which would threaten their standings.
Of course the DES totally miss the point when they say
The Department for Education and Skills said more pupils were studying maths.
More than what? Such is the pressure of those league tables that I can totally believe this story. I wonder sometimes if we shouldn’t rename this country Wonderland and then find an Alice who can make sense of it all.
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^